题目大意
一个欧拉图,从 $1$ 出发的欧拉路径个数。 $n \leq 100$
题解
这种结论题可能只有知道结论才能做。
首先我们求出一个 $1$ 点为根的内向生成树: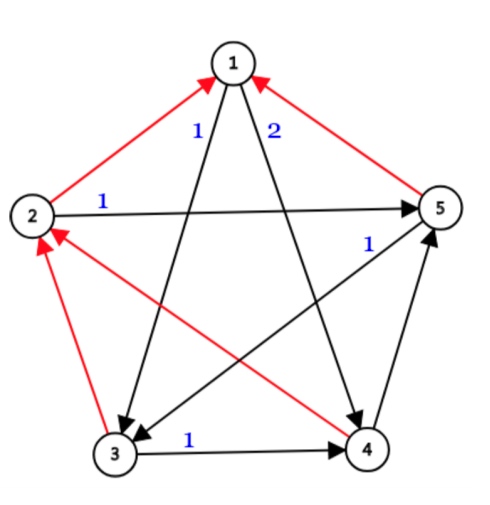
引理 1:每一个这样的生成树都可以对应若干个方案 且不同的生成树对应的方案一定没有交。
我们考虑从两个方向来证明:
生成树 $\to$ 欧拉回路
我们对于每个点 如果存在未走过的非树边就走过去 否则走树边 这样构造显然是一个欧拉回路 且满足引理 1。
欧拉回路 $\to$ 生成树
把每一个点最后走的边作为树边 这样构造显然是一个内向树 且满足引理 1
设每个点的出度为 $out_i$
根据证明过程我们也可以得到每一个内向树一定对应了 $out_1!\prod_{i=2}^n (out_{i}-1)!$ 种方案。(也就是每个点安排一下出边的顺序)
设 $A_i$ 表示以 $i$ 为根的内向树的生成树个数 答案就是 $A_1out_1!\prod_{i=2}^n (out_i-1)!$
有向图的生成数个数:
外向树:用入度矩阵-邻接矩阵
内向树:用出度矩阵-邻接矩阵
注意是删去根所在的行列 然后跑行列式。
Code:
const int MAXN = 100+5;
const int MAXM = 1e6 + 5;
const int ha = 1000003;
int n;
namespace Matrix_Tree{
int a[MAXN][MAXN];
inline int qpow(int a,int n=ha-2){
int res = 1;
while(n){
if(n&1) res = 1ll*res*a%ha;
a = 1ll*a*a%ha;
n >>= 1;
}
return res;
}
inline int inv(int x){
return qpow(x);
}
inline void add(int u,int v){
a[u][u]++;a[u][u] %= ha;
(a[u][v] += ha-1)%=ha;
}
inline int det(){
int ans = 1;
FOR(i,2,n){
int tmp = i;
FOR(j,i,n-1) if(a[j][i]) {tmp = j;break;}
if(tmp != i) std::swap(a[tmp],a[i]),ans = -ans;
FOR(j,i+1,n){
if(!a[j][i]) continue;
int div = 1ll*inv(a[i][i])*a[j][i]%ha;
FOR(k,i,n) (a[j][k] += ha-1ll*a[i][k]*div%ha) %= ha;
}
}
ans = (ans+ha)%ha;
FOR(i,2,n) ans = 1ll*ans*a[i][i]%ha;
return ans;
}
};
using namespace Matrix_Tree;
int in[MAXN],out[MAXN];
int fac[MAXM];
inline void Solve(){
FOR(i,1,n) FOR(j,1,n) a[i][j] = 0;
FOR(i,1,n) in[i] = out[i] = 0;
FOR(i,1,n){
int t;scanf("%d",&t);
while(t--){
int to;scanf("%d",&to);
in[to]++;out[i]++;
add(i,to);
}
}
if(n == 1 && out[1] == 0){
puts("1");return;
}
FOR(i,1,n) if(in[i] != out[i]) {puts("0");return;}
int ans = det();
if(ans == 0){
puts("0");return;
}
FOR(i,2,n) ans = 1ll*ans*fac[out[i]-1]%ha;
ans = 1ll*ans*fac[out[1]]%ha;
printf("%d\n",ans);
}
int main(){
fac[0] = 1;
FOR(i,1,MAXM-1) fac[i] = 1ll*fac[i-1]*i%ha;
while(~scanf("%d",&n) && n) Solve();
return 0;
}Bouns:要求循环同构
也就是 $1\to 2 \to 1 \to 3$ 等价于 $1 \to 3 \to 1 \to 2$。
发现实际上就是 $1$ 走的第一条边是啥。所以答案变成 $A_1\prod_{i=1}^n (out_i-1)!$
