题意

给你一个左边 $a$ 个点 右边 $b$ 个点 有 $m$ 条边的二分图。现在要求你给每一个边染色 使得每个点的所有边的颜色互不相同。要求使用的颜色最少 输出一种方案。

$a,b \leq 1000,m \leq 10^5$

题解

猜结论好题

很容易可以发现度数最大值是答案的一个下界。但其实它也是答案的上界。接下来我们将会基于一组构造来证明它（这组构造就是要求你输出的方案）

我们依次考虑每一条边，每次来了一条新边 $(u,v)$ ，我们先判断一下端点没有被用过的颜色最小值 记为 $t_0,t_1$。如果 $t_0 = t_1$ 那么这条边的权值就是 $t_0$ 就好了。否则我们需要调整。

我们钦定 $t_0 < t_1$ 考虑我们强制让这条边的颜色为 $t_0$ 那么 $v$ 这个点就会出现两个点颜色为 $t_0$，但是 $v$ 是有 $t_1$ 这个颜色可以使用的。于是我们找到 $v$ 这个点另一条颜色为 $t_0$ 的边，将其修改为 $t_1$ 即可。注意到这样也可能违反规则 我们只需要按照这个规则继续递归下去即可。最终一定会到达一个点 它递归不下去了 就直接把颜色赋值。

发现这样每个点的颜色编号都不会超过最大度数，所以符合题意。

搞一个图解：

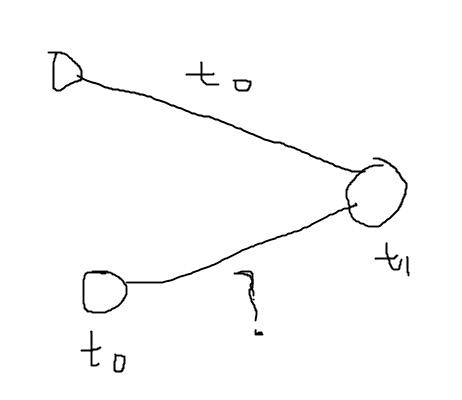
"?"边是这次要赋值成 $t_0$ 的边

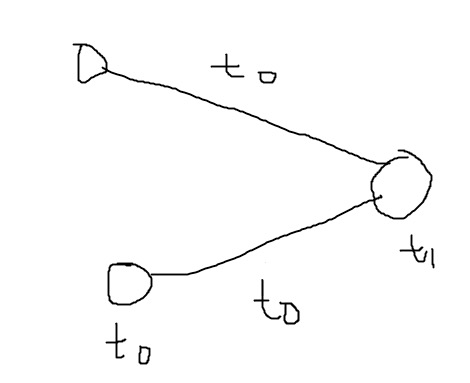
这样 右边这个点产生了冲突 于是我们转而去解决右边这个点的冲突

然后递归上去 直到某一个点没有冲突（根据二分图性质 显然有这样一个点）

每个边需要 $O(n)$ 的时间，总复杂度是 $O(nm)$ 的。

Code：

const int MAXN = 1000+5;
const int MAXM = 2e5 + 5;
int f[2][MAXN][MAXN];// 部 点 颜色
int du[2][MAXN];
int g[MAXN][MAXN];
int ans[MAXM];

inline void work(int a,int b,int u,int v,int x,int y){
    // 中间一个无色边 端点空闲的颜色分别是(x,y) （递归修改的时候先抹去颜色）
    int to = f[b][v][x];
    f[a][u][x] = v;f[b][v][x] = u;
    if(!to) f[b][v][y] = 0;
    else work(b,a,v,to,y,x);
}

int main(){
    int a,b,m;
    scanf("%d%d%d",&a,&b,&m);
    FOR(i,1,m){
        int u,v;scanf("%d%d",&u,&v);
        g[u][v] = i;
        du[0][u]++;du[1][v]++;
        int t0=1,t1=1;
        while(f[0][u][t0]) ++t0;
        while(f[1][v][t1]) ++t1;
        if(t0 == t1) f[0][u][t0] = v,f[1][v][t1] = u;
        else work(0,1,u,v,t0,t1);
    }
    int mx = 0;
    FOR(i,1,a) mx = std::max(mx,du[0][i]);
    FOR(i,1,b) mx = std::max(mx,du[1][i]);
    FOR(i,1,a){
        FOR(j,1,mx){
            if(f[0][i][j]) ans[g[i][f[0][i][j]]] = j;
        }
    }
    printf("%d\n",mx);
    FOR(i,1,m) printf("%d ",ans[i]);puts("");
    return 0;
}

作者太菜了图太丑了别喷我 QAQ