A
我们把天数分成会被禁言和不会被禁言的两类,首先如果选择了禁言的那些天我们一定会去选择最大的那些。于是我们枚举选前多少个禁言的,假设选了 $k$ 个,那么相当于我们要从剩下的 $n-k$ 天中选一些天塞到被禁言的那些位置去,要选 $dk$ 个。首先先选择说了会被禁言的那些天,然后在不会被禁言的填里尽量选择最小的。
B
由于每个点只能往外连一条边,设第 $i$ 个点连向的点为 $p_i$,要求每个点都在一个环内我们自然想到 $p$ 是一个排列。
我们可以考虑哈希:给每一个点赋一个随机权值,合并两个哈希值的时候相乘。然后我们预处理 $g_{i,j}$ 表示度数为 $i$ 的点选择第 $j$ 条边得到的集合的哈希值。
然后我们可以 $k!$ 枚举这个 $c_k$ ,然后 $O(k)$ 判断。
注意这里要写多模,反正我写了五模。
C
要求最大值最小,考虑二分答案 $mid$。
下面就是问你是否存在一个串 $t$ 满足 $\forall i ,dis(i,t) \leq mid$ 了。
我们考虑如何快速计算 $dis(s,t)$:很容易发现字符串的形态是无用的(如果同时存在 $b,n$ 一定有一个位置是 $bn$ 或者 $nb$)。所以现在相当于每个串是一个二元组 $(x,y)$,每次操作可以给单独一个数加减一,给整体加减一,要求时刻 $x,y \geq 0$,问最小操作步数使得两个二元组相等,
可以发现如果两个二元组 $(a,b),(c,d)$ 如果 $a-c$ 和 $b-d$ 同号,那么相当于有可以共同加减一的部分,答案就是 $\max\{|a-c|,|b-d|\}$;否则没有共同加减一的部分,答案就是 $|a-c|+|b-d|$。
所以我们得到:
$$ dis((a,b),(c,d)) = \begin{cases} \max\{|a-c|,|b-d|\},& (a-c)(b-d) \geq 0\\ |a-c|+|b-d|,& (a-c)(b-d) < 0 \end{cases} $$
设输入的第 $i$ 个串代表的点为 $(x_i,y_i)$,如果一个点 $(x,y)$ 合法,首先显然要满足
$$ \forall i \in [1,n],\max\{|x-x_i|,|y-y_i|\} \leq mid $$
但是发现这样没有限制好异号的点,我们考虑对于这样的点(即 $(x-x_i)(y-y_i) < 0$),有额外限制:
$$ |x-x_i|+|y-y_i| \leq mid $$
我们考虑把每个二元组看做一个点:考虑点 $P$ 能覆盖到的区域是什么样的:
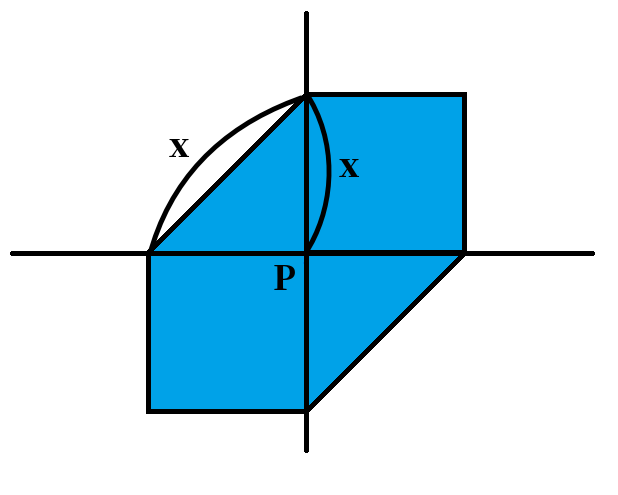
(这里的 $x$ 就是二分的答案 $mid$)
现在我们回来考虑一下如何去判定是否存在一组这样的点:考虑把限制拆开写:
首先考虑对所有点的限制:
$$ \begin{aligned} &|x-x_i| \leq mid,|y-y_i| \leq mid\\ &\Rightarrow -mid \leq x-x_i \leq mid,-mid \leq y-y_i \leq mid\\ &\Rightarrow x \in [-mid+x_i,mid+x_i],y \in [-mid+y_i,mid+y_i] \end{aligned} $$
然后考虑对异号点的特殊限制,我们肯定要考虑将其写成一个对所有点都满足的限制(对同号点无论如何都满足,并且恰好限制到异号点)。
对于 $|x|+|y| \leq lim$ 我们可以写成 $|x-y| \leq lim$。那么我们设 $x,y$ 同号,$|x-y| \leq |x+y|$,所以这个限制是对的。
所以可以写成对所有点还有限制:
$$ \begin{aligned} &|x-x_i-y+y_i| \leq mid\\ &\Rightarrow -mid \leq x-x_i-y+y_i \leq mid\\ &\Rightarrow -mid+x_i-y_i \leq x-y \leq mid+x_i-y_i \end{aligned} $$
现在相当于有这些不等式,我们确定出 $x,y,x-y$ 的范围后就可以方便判断是否有解。
最终输出方案时,我们假设通过上面的不等式得到了 $x \in [xl,xr],y \in [yl,yr],x-y \in [xyl,xyr]$,我们枚举一个 $y$ ,可以得到 $x \in [xl,xr]\cap[xyl+y,xyr+y]$。取一组满足 $x,y$ 至少有一个非 $0$ 的解即可。
D
发现对于一条边 $(u,v)$ 如果 $h_u \neq h_v$ ,设 $h_u < h_v$,相当于有一条 $u \to v$ 的有向边;否则是一个待确定方向的边。
我们先考虑如果所有的边都是有向边怎么做:首先答案的一个下界是 $\sum_{i=1}^n t_i(in_i+out_i)$,其中 $in_v,out_v$ 分别指 $v$ 的入度和出度。但是我们发现在每个点上我们可以把一些出度和入度匹配,每匹配一对就可以减少一次选择这个点的代价,所以答案就是那个下界减去 $\sum_{i=1}^n t_i\min\{in_i,out_i\}$。
现在我们有一些边没有被定向,显然暴力枚举不太行,所以要考虑 dp:
首先把有向边全删掉,于是形成了一些未确定方向的边形成的森林,显然它们之间是独立的。你现在的目标是最大化配对能减少的代价。
发现我们在处理一个点的时候只需要知道它到父亲的边的顺序就可以了,于是我们设 $f_v$ 表示 $v$ 父亲边向上的最大收益,$g_v$ 表示向下。
转移的时候我们先处理完所有儿子,然后枚举一个父亲边的方向。接下来我们考虑父亲边向上的情况:
我们考虑去枚举儿子中父亲边向上的数量 $x$,设儿子的数量为 $x$ ,那么向下的数量显然为 $s-x$,带来的收益就是 $t_i\min\{x,s-x+1\}$。然后问题变成了选择一个儿子的大小为 $x$ 的子集 $S$ 最大化 $\sum_{v \in S} f_v + \sum_{v \not \in s} g_v$。
我们可以先假设全都选择 $g$ ,然后每一个儿子改变到 $f$ 的收益就是 $f_v-g_v$,对这个从大到小排序就可以 $O(1 ) $ 回答每个询问了。
E
大部分图片都摘自 CF 官方题解。
感性理解题目
考虑一个具体的例子:$a = [1,2,2,2,1,1,2,2]$ ,我们按照以下两种方式折叠:
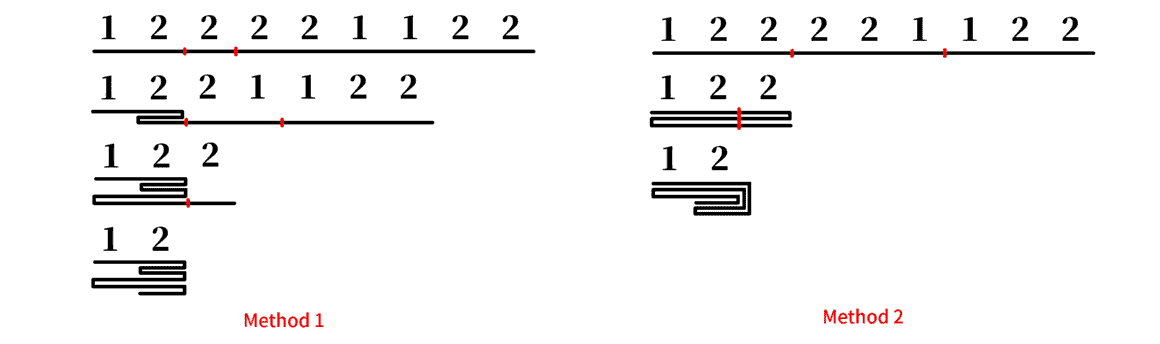
可以发现这两种不同的方式本质是等价的,因为我们有变换:

定理 1:所有折叠方式都可以通过类似移动环的方式变成 ”Z“ 字型折叠结构。
所以我们可以从左到右折叠,折到不能折的时候就一定是一种最优的方案。
所以我们可以得到结论 2:
定理 2:所有折叠方案,只要把能折的部分都折了就一定达到了最优的折痕数量。
所以我们可以考虑构造一种从左到右的折叠方案。
从左到右的好处是每次只折叠了一张纸:这样就只需要计算折叠次数而不用计算每次折了几张纸了。
这里建议大家动动手自己折一折纸,感性理解一下折纸的本质是什么。
X-Y-X 串
我们假设现在有这样的一个区间:
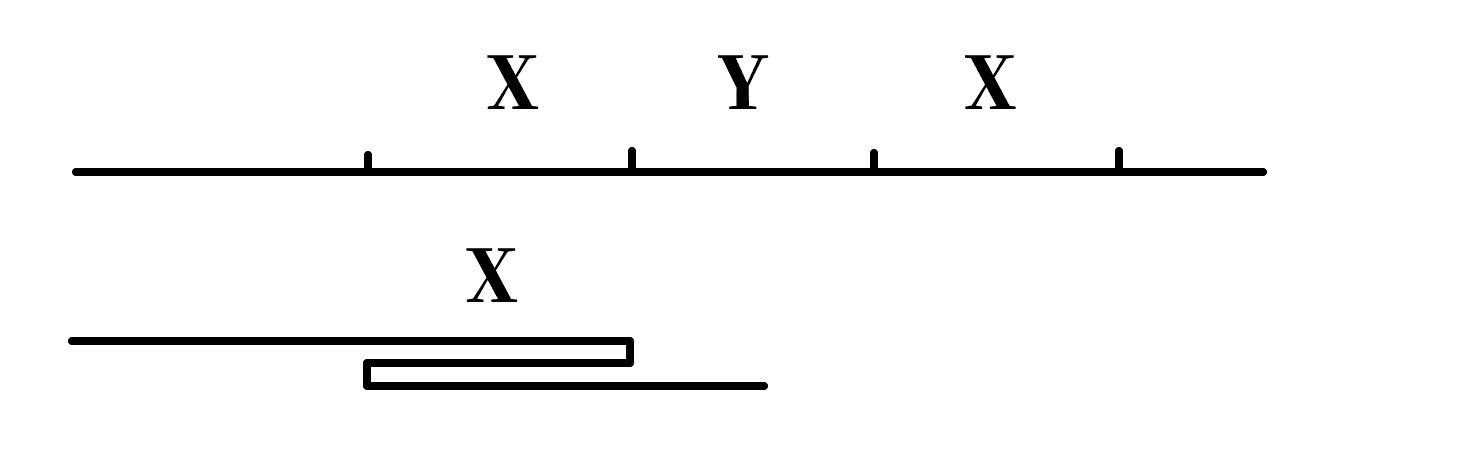
其中 $XY,YX$ 都是回文串。
我们定义真 X-Y-X 串,满足它不存在一个真子串满足是 X-Y-X 串。
根据定理 2,我们不妨想到可以先把所有形如 X-Y-X 格式的区间都给折了,然后再去处理剩下的区间。接下来分两步走:
- 如何快速找出 X-Y-X 型区间?
- 如何处理没有 X-Y-X 型区间的串?
如何找出所有 X-Y-X 串
先给出一个引理:
引理 1:对于两个偶回文子串 $[l_1,r_1],[l_2,r_2]$ 如果 $[l_1,r_1]$ 包含 $[l_2,r_2]$ 的回文中心且 $[l_2,r_2]$ 包含 $[l_1,r_1]$ 的回文重心,那么 $S$ 一定包含 X-Y-X 串。
如下图构造即可,红色区域即为一个 X-Y-X 串。
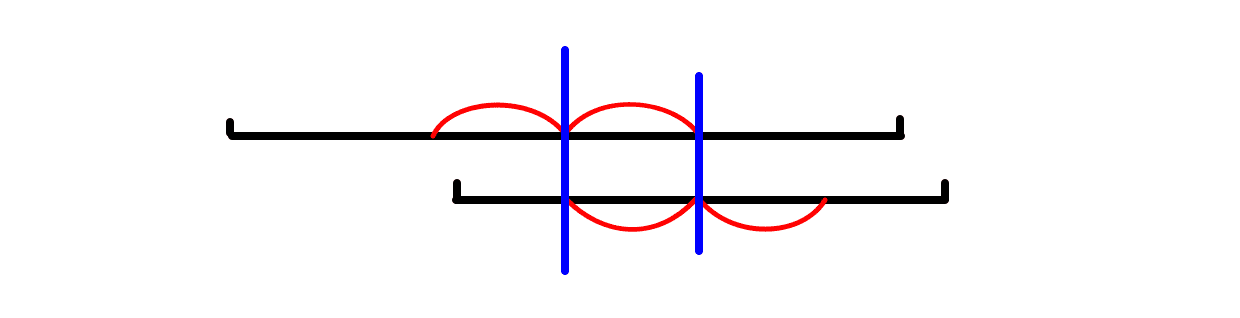
由于要多次询问,我们考虑一个一个加入字符。现在我们考虑上一次的串为 $b$,加入一个新字符后的串为 $b'$,假设 $b$ 已经缩起来了所有的 X-Y-X 串。
定理 3:$b'$ 最多有一个 X-Y-X 串。
如果 $b'$ 有 $>1$ 个 X-Y-X 串,那么只有三种情况:
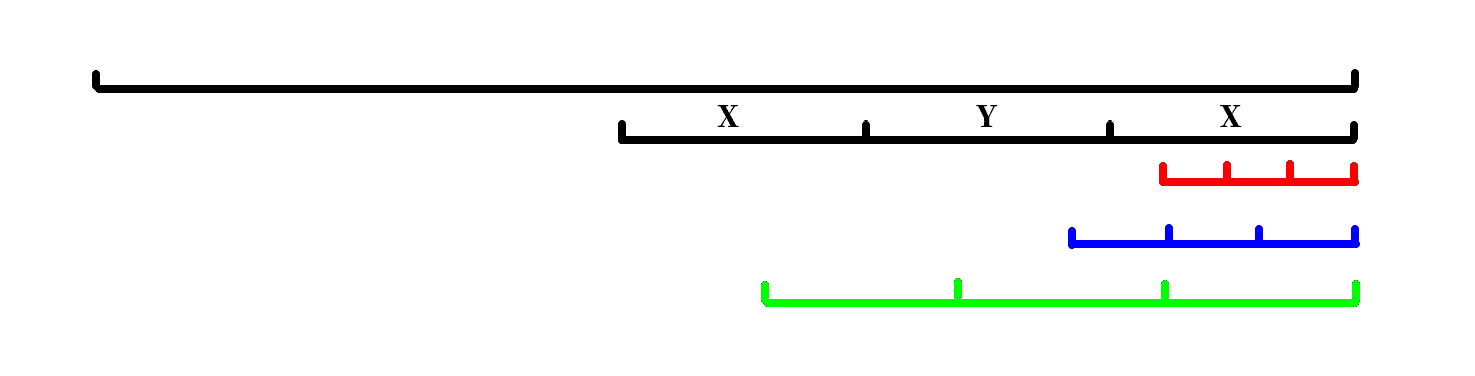
- 黑和红:把红对称到黑色的 $Y$ 里,$b$ 内有 X-Y-X 串,矛盾。
- 黑和蓝:蓝的 $XY$ 和黑的 $YX$ 满足引理 $1$,矛盾。
- 黑和绿:绿的 $XY$ 和黑的 $XY$ 满足引理 $1$,矛盾。
容易发现这个 X-Y-X 串是真 X-Y-X 串。
于是如果我们想维护出折掉所有 X-Y-X 的串,就可以枚举所有的后缀,判断是否是即可。
但是这样的单词复杂度是 $O(n)$ 的,总复杂度就是 $O(n^2)$ 的,显然过不了。
我们继续发现一些性质:
定理 4:真 X-Y-X 串只会有一个偶回文后缀(即 $YX$)
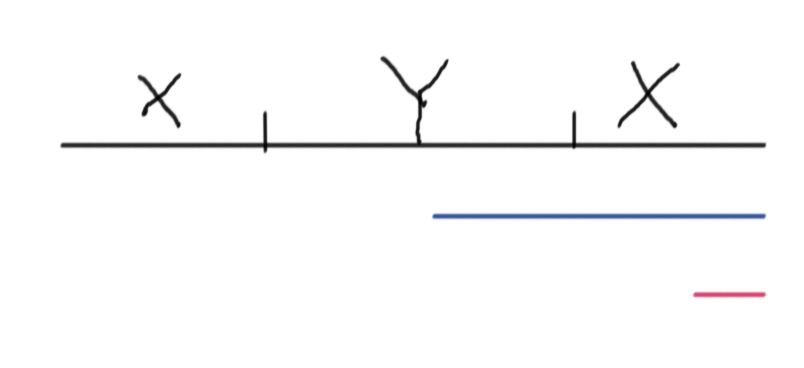
如果是蓝色:根据引理 $1$ 导出矛盾
如果是红色:直接在 $XY$ 中找到一个串 $aba$。
结合定理 $3$,我们可以发现 $b’$ 的 X-Y-X 串一定由最短偶回文后缀产生,因此我们只要快速维护处 $b'$ 的最短偶回文后缀即可。
定理 5:$b'$ 的偶回文后缀有 $O(\log n)$ 个。
因为偶回文后缀之间不能出现引理 $1$ 的情况(要不然前面就有 X-Y-X 串了),于是一定形如这样分布:
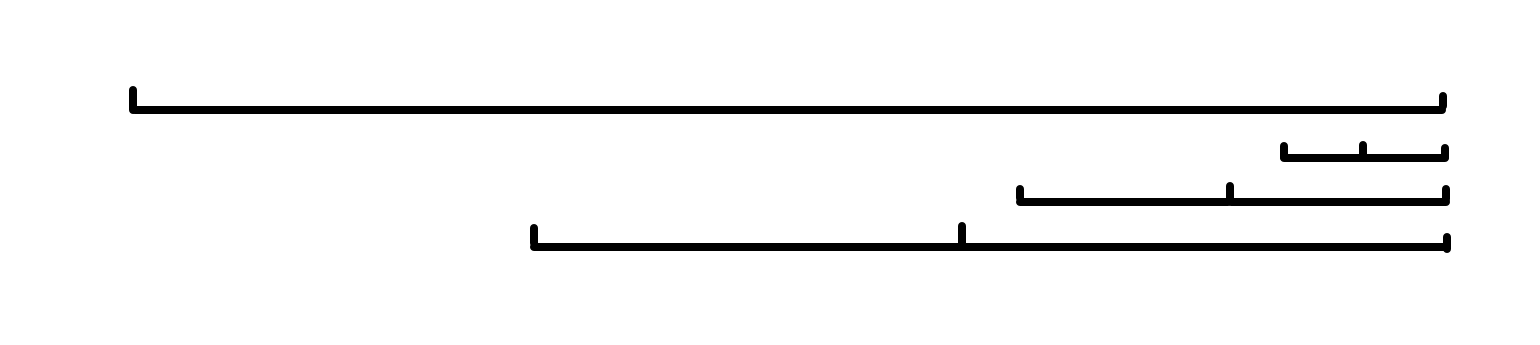
不难发现每次长度递增,所以个数是 $O(\log_2 n)$
所以我们可以用 vector 维护处所有的回文偶后缀,每次加入一个新字符的时候首先去更新当前的 vector,然后分类讨论:
- 如果出现了新的 X-Y-X 型的串:记录下来,并且将对应的后缀删去
- 如果未出现 X-Y-X 型串:就去更新下面即将要说的其他信息就好了。
每次更新 $O(\log n)$。
如何处理没有 X-Y-X 型区间的串
没有 X-Y-X 我们只能考虑对折,也就是每次操作一个偶回文前缀或者偶回文后缀。
考虑偶回文后缀的情况:
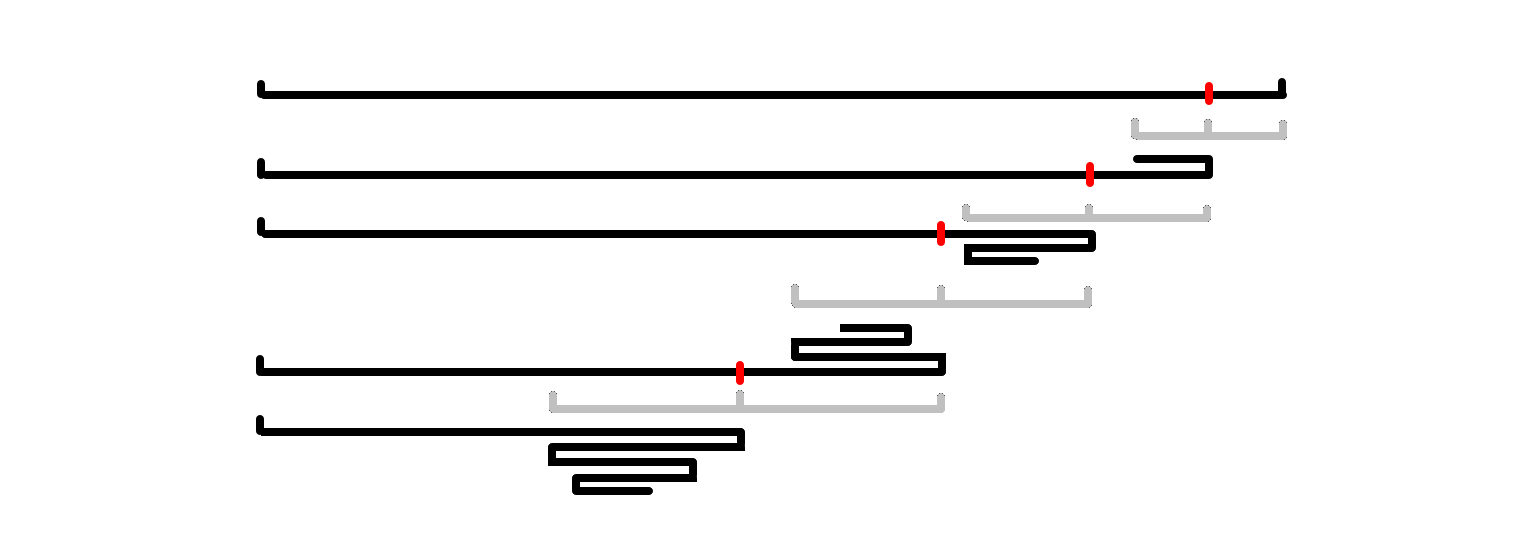
根据定理 $1$ 我们每次肯定去折叠最小的才能达到 $L$ 型。所以每次折叠的后缀长度一定是严格递增的。前缀也是类似的。
定理 6 对于没有 X-Y-X 的串,最多被折叠 $O(\sqrt n)$ 次。
只需要注意到等式 $\sum_{i=1}^n i = \frac{n(n+1)}{2}$。
于是我们分类讨论前缀和后缀:
- 对于后缀:从 vector 中就可以得到最短偶回文后缀。
- 对于前缀:设 $q_i$ 表示区间 $[1,i]$ 从开头折叠能最远折到哪里,$c_i$ 表示折叠次数。
每次加入一个点的时候:
- 对于前缀:如果可以继续跳的话一定代表了 $[q_i,now]$ 是一个偶回文串,直接判断即可
- 对于后缀:直接用 vector 信息即可,不需要特别维护。
如何回答询问
首先我们先能 $O(1)$ 得到 X-Y-X 的数量,记为 $\alpha$。
然后我们可以通过 $c_i$ 得到前缀可以折多少,然后就暴力用 vector 里存的最短偶回文后缀的信息暴力跳,根据定理 $6$ 我们只需要跳 $O(\sqrt n)$ 次就停下来了,设有效跳了 $\beta$ 次,答案就是 $\alpha+\beta+c_i$。
单次询问复杂度 $O(\sqrt n)$。
完成了!
总结一下:
维护 $q_i$ 表示 $[1,i]$ 每次折叠最小前缀可以达到的最远位置,$c_i$ 表示次数,维护 $xyx$ 表示 X-Y-X 串的数量,对于每一个位置再维护一个 vector $v_i$ 表示当前的后缀偶回文串是哪些。
每次加入一个新字符 $c$,对应更新 vector 后:
- 如果产生了新的 X-Y-X 串(一定是一个后缀):直接删除掉一些后缀即可。
- 如果未产生新的 X-Y-X 串:更新 $q_i,c_i$ 即可。
最终 $O(\sqrt n)$ 回答询问。
这个题建议配合代码理解使用(因为我表达能力可能不是很好)。
