计算几何看了一下午自闭了

A

我们先考虑如何将一个串变成全部相等：我们从前往后确定，假设我们让前 $i$ 位都满足条件了，假设 $a_i \neq a_{i+1}$，我们就操作 $i$ 前缀，这样就相等了。

那么如果都变成 $0$ 的话就看看最后是全 $0$ 还是全 $1$ 就好了。这样操作次数是 $\leq n$ 的。

我们对 $s$ 这样做，对 $t$ 这样做，然后把 $t$ 的操作倒过来对 $s$ 做即可。操作次数 $\leq 2n$。

B

我们找到序列的最大值，发现最大值后面的数一定和最大值是一组的。

所以我们经过这样的拆分，相当于变成了有若干个数字 $x_i$，问你能否选出一个集合 $S$ 满足 $\sum_{i \in S} v_i = n$。背包即可。

C

首先有 $n$ 个数但是有 $n+1$ 个颜色，肯定有一种颜色是没有出现过的，可以把它叫做工具人。

首先我们必须选出 $x$ 个位置满足这 $x$ 个位置填的数和 $b$ 对应位置相等，然后选出 $y-x$ 个位置填上一些数，满足如果这 $y-x$ 个位置和剩下的颜色连边，能形成完美匹配并且这 $y-x$ 对应位置的数不相等。剩下的位置填工具人就好了。

先考虑如何判断 $y-x$ 个位置是否都是合法的：每次同时在 $a$ 序列和 $b$ 序列中同时删除一对一样的数，一直到删光或者删不动位置。相当于要做一个匹配。如果最大值 $< \frac{n}{2}$ 就能都匹配上，否则只能匹配 $n-\frac{n}{2}$ 对，所以我们第一步操作要尽量要求最大值尽量平均。

于是可以得到我们第一步的贪心操作：每次选择当前出现次数最大的数，将其出现次数 $-1$。

然后操作二我们可以把相同数字排到一起，shuffle $\frac{n}{2}$ 位然后对应填上就能得到最大的配对数量了，最后根据题目要求再填一些工具人就好了。

D

设蛇的长度为 $L$，我们称一个点为特殊点当且仅当有三条以这个点为端点的不相交的长度 $\geq L$ 的链。

首先我们可以发现如果一个蛇的头（或尾）在这个特殊点上那么这个蛇一定可以翻转过来，并且如果一个蛇的头（或尾）已经在特殊点上了，一定可以移动到其他特殊点上。都是可以构造证明的。

于是我们首先通过dp（up and down）找出一个关键点，然后以这个关键点为根，假设现在的蛇是 $(u,v)$ 我们每次贪心地把 $u$ 移动到子树内最深的叶子，$v$ 移动到子树内的叶子...... 发现执行 $O(n)$ 次一定能变成 $u,v$ 有祖先关系或者是无解。倍增加速跳祖先这一过程即可（长链剖分也可以）。

E

考虑一维的情况怎么做：

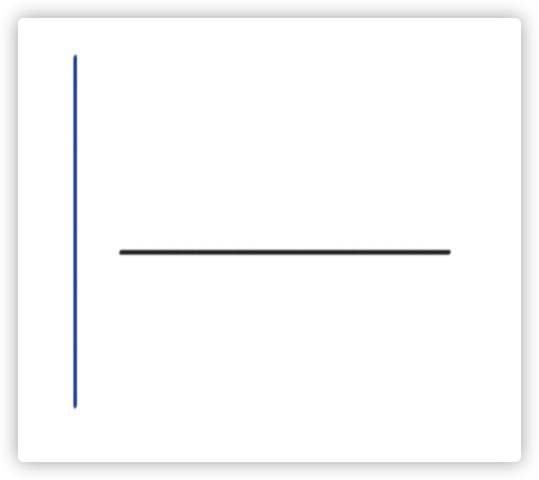
这样显然是没有减少任何长度的。

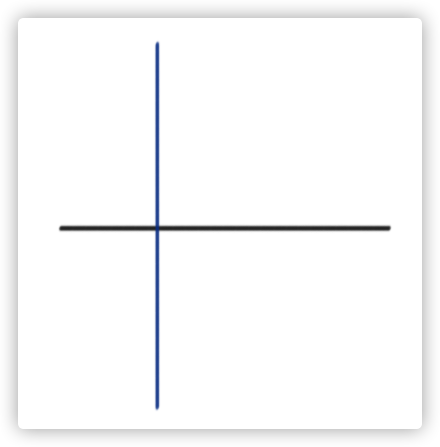
这样就会减少较小的这一段。

我们考虑把情况都转化到左边：如果减少的是右边较小的这一段，我们可以看成先减掉左半边全部，再加上右半边到询问的线的距离，也就是：

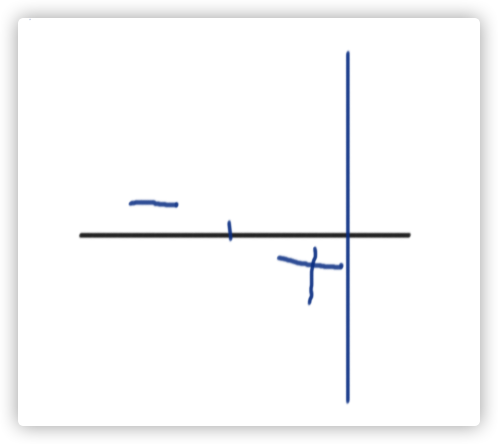
然后现在你就会了一维的情况：给前一半的直线赋一个负数，后一半正数，把询问离线下来做扫描线，做一个类似前缀和的东西就好了。

考虑扩展到二维：首先我们观察结论是否还成立：

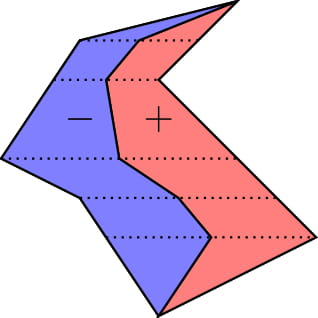
我们对于每一个点，都做一条过该点平行于 $x$ 轴的线段，一直到多边形边界才停止。

取这些线段的中点并连接起来，发现左边就是负贡献，右边就是正贡献。

考虑如何算一条线左边的面积。

然后对于每一块都是一个线性函数的积分，于是可以维护所有积分加起来

发现只有在每一个点才会让面积的导数加上一些东西，所以就直接扫描线过去就可以了。

然后这个题相当于在中间加了若干条从负贡献变到正贡献的边，也对着处理一下就行了。

可以看一下代码辅助理解。