A

按照题意模拟，每次让小的加上大的就行了，进行 $O(\log n)$ 次一定能求出来一组解。

观察迭代方式我们发现操作 $i$ 次后的数对可以表示成 $(f_{i-2}a+f_{i-1}b,f_{i-1}a+f_{i}b)$（其中 $f$ 是斐波那契数列且 $f_0=1$）。

B

显然一种很好的方式是把匹配同一位置的字符匹配在一起，方案数就是每个位置匹配的字符的个数的乘积。

根据一些基本的不等式理论，如果和（长度）确定的话一定是尽量平均乘积尽量大。

首先我们假设所有的出现次数都相等 $=x$，那么可以造出 $x^{10}$ 种不同的串。如果还是不够的话，就从第一个位置开始不断加一个字符，加到够了就行。

C

随便构造。我的构造方法是首先考虑 $n=1$，就可以轻易得出一种构造方案：

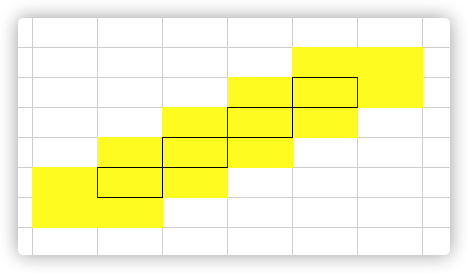
D

考虑如果设 $a > b$，那么可以注意到如下实施：

$$ (a+t)^2 + (b-t)^2 = a^2+b^2+2t^2+2at-2bt > a^2+b^2 $$

所以我们贪心地想肯定是尽量将小的数加到大的数上去。

我们观察我们这个操作实际上是在把所有不同的位都移动到大的上去。

于是我们考虑对于每一位维护一个 set，维护这一位是 $1$ 的值的位置有哪些。

从后往前枚举一个数的每一位，如果这一位为 $0$ 就从它前面找一个这一位是 $1$ 的数，把这两个数操作一下。

如果暴力每次枚举一个数 $O(n)$，枚举一位 $O(\log n)$，找到前面的一个数并把这个数删掉，修改这个数，然后插入 $O(\log^2n)$。咋一看这个复杂度是 $O(n \log^3n)$ 的，其实不然：我们只需要修改这个数变动的位置对应的 set 就好了。因为我们发现每个数只会修改 $\log n$ 个 set，复杂度就是 $O(n \log^2 n)$。

E

可能容易看漏一个条件：每个点最多只有两条出边。

我们考虑按照拓扑序枚举，每次判断这个点是不是已经有距离为 $2$ 的前驱了，如果有就删去。

首先这样删一定能保证剩下的点距离至多是 $1$。

然后发现我们设 $V_1$ 表示入度为 $0$ 的点集，$V_2$ 表示 $V_1$ 相连的点集，$V_3$ 表示 $V_2$ 相连的点集，发现我们只需要删除 $V_3$ 就好了，而根据出边至多为 $2$，可以得到 $V_1 \geq 2V_2 \geq 4V_3$，也就是 $V_3 \leq \frac{4}{7}(V_1+V_2+V_3)$，然后删掉这三种点接着做，发现删掉的点一定 $\leq \frac{4}{7}n$。

F

首先脑补一下我们如果走的最后一步选择了 $k$ 个点，如果有长度为 $k$ 的连续段，那么相当于这一步没有用，可以删去。

那么我们贪心地思考最后一步如果选择了 $k$ 说明这个环里一定是若干个 $\leq k-1$ 的连续段。我们不妨猜想每一步的 $k$ 是相等的，在最后一步先手操作完之后，后手一定会拿掉长度为 $k-1$ 的一段 $1$。所以我们可以得到 $R(n) = n-(k-1)-\lceil \frac{n}{k}\rceil$。构造就是我们先选出 $\lceil \frac{n}{k} \rceil$个点作为不能选的点，重复每次选择 $k$ 个没有被选过的点，这样会让答案每次 $+1$。

至于这个答案上界的一个严谨的证明：考虑最后一步操作前我们 $1$ 的数量为 $x$，操作了长度 $k$。那么根据这一步是有用的限制，一定要满足 $\frac{x+k}{k-1} \leq n$，也就是 $x \leq n-k-\lceil \frac{n}{k} \rceil$。然后操作最后一步答案会 $+1$，所以证明了 $R(n) \leq n-k-\lceil \frac{n}{k}\rceil +1$，然后运用上述构造即可取到上界。

G

可以把移动多米诺骨牌看做空沿着多米诺骨牌的长边移动。也就是假设这个骨牌为 $(x,y),(x+1,y)$，那么连边 $(x-1,y) \to (x+1,y),(x+2,y)\to (x,y)$。观察这个图有什么性质：

• 是一个有根树森林：因为每个点只有唯一的入边，可以将入边当做树上的父亲
• 黑白染色后两个点在不同的连通块内，这个显然，因为每次跳都不改变奇偶性

所以相当于对于每个骨牌的两个点 $x,y$，从 $x$ 的子树和 $y$ 的子树中任选两点都可以组成方案。

求出 dfn 序之后相当于是一个矩形面积并问题，扫描线+线段树即可。

发现这里有几个细节：

1. 线段树部分因为删除的区间一定是之前加入过的，只需要在每个节点上维护现在有的区间个数就好了
2. 因为这里的点对显然是无序的，并且两个点一定不是祖先关系，所以我们要求第一个区间的 dfn 小于第二个区间的 dfn 才能保证答案正确。（扫描线一定要注意是否有序！！！）

H

H1

这个之前 ZR 网课听过有模糊的印象。。。稍微想一想就想起来了。

首先这个问题可以显然地转化为网络流问题：

中间每条边流量是 $1$ 然后可以源点向红色点连 $1$，蓝色点向汇点连 $1$。

首先为了让接下来的讨论只和这个图里的边有关，不妨把源汇连出的边流量设为 $\infty$，这样就无需考虑了。

然后根据最大流=最小割，我们将其转化为最小割问题。

这个图的最小割问题的本质就是给图中的每个黑色小点赋两种颜色之一，如果相邻两个点颜色不同答案就 $+1$。

我们先不考虑边界上如何选择，假设在中间有这样的情况：

显然把中间凸出来那一块红色填成蓝色花费会更低。所以我们在非边界上蓝红色连通块一定是成行或成列的。

发现边界上的边割掉就等价于把边界上的点改个颜色，于是现在问题变成了：

我们可以修改边界上的点的颜色，代价为 $1$ ，我们必须保证每行或者每列颜色都是相同的，如果相邻两个颜色不相同答案 $+1$，求最小代价。

可以枚举是行相同还是列相同后简单 dp：设 $f_{i,0/1}$表示考虑到第 $i$ 个，上一个是什么颜色，转移的时候需要用到这个位置上下的边界的颜色转移即可。

H2

带翻转颜色的修改，显然我们要用线段树维护标记。

首先分治里我们只需要记录两个边界的颜色就好了，合并的时候枚举一下中间的颜色即可。

对于这种带翻转颜色的，我们就可以对于每个点维护处翻转颜色前后的情况。对于这个题，如果我们让每列都相同，我们要维护四种情况：上下都没翻转，上面翻转，下面翻转，上下都翻转。翻转的时候打个标记，交换对应的 dp 数组就行了。

然后要顺带着维护上下边界的颜色情况，然后还要对行相同的情况类似做一遍。。反正写就完事了。