A
从小到大填就好了。暴力求一下周围点的 mex。由于每个边只会被访问一次,复杂度 $O(m \log m)$。
B
维护两个集合 $L,R$ ,我们保证 $L \geq R$。
首先从大到小排序,每次遇到一个新的数,如果 $L=R$ 就加到 $L$ 集合中,否则先加到 $R$ 集合中,然后不断从后向前合并 $R$ 集合,然后判断 $L,R$ 最后一位是否相等,再不断消去末尾相等的位置即可。(因为 $L,R$ 按照这样的维护方式都是不增的,并且一开始给 $L$ 加了一个大数说明无论怎么凑只能先凑到 $L$ 最小的那个数)。
C
首先枚举答案,相当于变成 check 能否使得所有的美丽值都 $\geq k$。
两个位置能连接相当于要求所有连接的地方 $0 \ldots k-1$ 位都是 $0$。
也就是说如果两个数能匹配,那就要求 $0 \ldots k-1$ 位是相同的。
首先建 $2^k-1$ 个点,于是可以对于每个块 $(u,v)$,连 $a_u,a_v$ 只保留 $0\ldots k-1$ 位的数代表的点,然后把 $(u,v)$ 连起来。求一个欧拉回路就好了。
D
首先这个树是长得形如若干条链的样子。
我们先考虑每个点如果保留它的贡献:设这个点是这条链上从远到进第 $j$ 个点,那么贡献就是 $(k-j-(j-1))d_i = (k-2j+1)d_i$。
根据这个式子我们可以看出:如果一条链选择的点 $\leq \lceil \frac{k}{2} \rceil$ 时,一定是从远到近;如果 $> \lceil \frac{k}{2} \rceil$ 时,一定是从近到远。设 $f(x)$ 表示选择 $x$ 的最优方案,不难看出 $f(x)$ 是凸的(增量逐渐减少),于是可以用类似闵科夫斯基和的方式求的答案:把所有增量排个序,取前 $k$ 大即可。
这种类型的贪心实际上是说有 $m$ 个凸函数 $f_i(x)$,要求
$$ \max_{i_1+i_2+\ldots+i_m = k} \sum_{j=1}^n f_j(i_j) $$
实际操作上就是把凸壳上每条边拆开,选择前 $k$ 大的斜率。
E
首先考虑如何 $O(n+m)$ 判断一个点是不是有趣的:相当于要求以这个点为根的 dfs 树只能有从下往上的返祖边。
这个 $20\%$ 的条件意味着如果我们随机 $T$ 个点去判断,如果都不是就输出 $-1$,错误的概率是 $\leq (\frac{4}{5})^T$ 的,取 $T \approx 50$ 就可以得到概率 $\leq 10^{-5}$ 了,足以通过。
考虑我们求出一个点 $r$ 之后如何去找出其他点:我们先以 $r$ 作为根建一棵 dfs 树出来,然后考虑每个点:
- 如果这个点的子树有 $\neq 1$ 条返祖边,那么这个点一定不合法
- 这个点合法当且仅当这个点子树内的返祖边指向的点是合法的
设这个点为 $x$,返祖边指向的点为 $y$。
充分性:
首先 $x$ 可以到达它在 $r$ 为根时的子树的所有点,由于只有一条返祖边,其他的点只能由 $y$ 到达。
首先知道 $y$ 一定可以到达 $x$ 子树外全部的点,而 $y$ 又是 $x$ 的祖先,所以 $y$ 一定能到达 $x$ 子树内的点。
必要性:
如果 $y$ 是合法的,那么 $x$ 就能到达全部点。并且如果想回到子树 $x \to y \to x$ ,不会出现两条不相交的路径。
所以我们可以先树上差分出每个点被多少条返祖边覆盖,然后求出子树内最往上的返祖边,判断即可。
F
考虑在序列 $W$ 上每次操作可以看成选择一个点 $x$ ,定义一个点控制的区间为包含这个点且这个点为最小值的极大区间。
那么操作可以看成每次把 $x$ 控制的区间左侧和右侧交换。于是我们可以考虑对 $W$ 建一棵笛卡尔树,把 $P$ 按顺序挂在 $W$ 的叶子节点上。
一个 $P=[3,4,6,2,1,5],W=[5,2,3,1,4]$ 的例子:
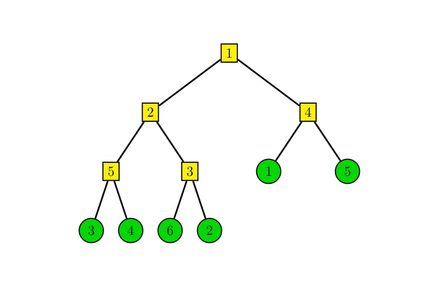
于是我们考虑如何去暴力计算答案:我们考虑让排列内任何一对逆序对 $(x,y)$ 的答案在它们的 lca 上统计,那么我们可以去枚举 lca,相当于每次可以选择交换子树,对答案的贡献是从左侧选出一个 $x$ ,右侧选出一个 $y$,$x>y$ 的对数。
但是我们发现 $W$ 是随机的,说明这个数期望树高 $O(\log n)$。
所以我们可以直接用线段树维护出每个节点子树内所有 $P$ 的信息(权值线段树)。
那么查询的时候就枚举一下是否交换分别查询就行了。
修改也可以暴力跳树高,是单次 $O(\log^2 n) $的。
