A

首先我们可以发现如果一个点是旅游城市，那么它的祖先也必然都是旅游城市（否则可以交换，答案不会变小）。

所以我们现在可以看成选了一个点 $v$ ，它带来的代价就是 $sz_v-dep_v$，排个序取前 $n-k$ 大就行了。

B

全排列枚举 $x,y,z$ 的大小关系，枚举第二大的那个数，直接通过双指针找到比它第一个大的和比它第一个小的数即可。

C

这种开头和结尾加字符的还是考虑区间 dp 比较好。

因为 $m \leq n$，我们可以在 $T$ 后面补上 $n-m$ 个通配符，然后设 $f[l][r]$ 表示用 $S$ 中前 $r-l+1$ 个匹配了 $T$ 中 $[l,r]$ 的方案数，转移直接枚举往前还是往后放就好了。

D

设数字 $i$ 出现的次数是 $a_i$，我们发现第一种权值本质是返回 $\sum_{i=1}^n \binom {a_i} 3$，第二种权值是返回 $\sum_{i=1}^{n-2} a_{i}a_{i+1}a_{i+2}$。

于是就有个显然的 $O(3n)$ 次询问的方法了。然后对着这个自闭了半天。

其实你发现题目给出了初始值，并且 $\binom {a_i} 3$ 是三次的，所以我们可以考虑差分降次。

那么发现我们如果询问 $i$ 两种权值的变化量分别是 $\binom {a_i}{2}$ 和 $a_{i-2}a_{i-1}+a_{i-1}a_{i+1}+a_{i+1}a_{i+2}$。发现我们两次询问一定可以求出一个 $a_i$，如果我们知道 $i-2,i-1,i+1$ 的值然后询问 $i$ 就可以递推出 $i+2$。于是我们发现只需要四次询问处理出 $a_1,a_2,a_3$，顺便递推出 $a_4$，然后询问 $3 \ldots n-2$ 就可以恰好 $n$ 次求出答案了。

但是我们发现如果某一个位置 $a_{i+1}=0$ 你就递推不下去了，所以我们考虑一开始先给 $3 \ldots n-1$ 加上 $1$，那么现在如果你在询问 $i$ 你能得到 $a_{i-2}a_{i-1}+a_{i-1}(a_{i+1}+1)+(a_{i+1}+1)(a_{i+2}+1)$

现在我们只需要能 $3$ 步求出 $a_1,a_2,a_3,a_4$ 就好了。

经过构造我们可以这样做：

1. 询问 $1$，得到 $a_2(a_3+1)$
2. 询问 $2$，得到 $(a_1+1)(a_3+1)+(a_3+1)(a_4+1)+1$，
3. 询问 $1$，得到 $a_1$ 和 $(a_2+1)(a_3+1)$

然后可以发现 $(a_2+1)(a_3+1)-a_2(a_3+1) = a_3+1$，所以可以求出 $a_3$，进而求出 $a_2$ 和 $a_4$，剩下的就可以愉快递推了（运用一开始询问的答案），这样也不会出现 $0$ 的情况了。

E

首先先注意一个 $O(2^m)$ 的朴素做法是求出一个线性基 $B$，设这个线性基的大小为 $|B|$，然后我们就可以 $O(2^m)$ 枚举所有可以组合出来的值。一个经典结论是每一个值都出现了 $2^{n-|B|}$ 次。如果加上折半搜索和 FWT 合并足以通过 E1 了。

E2 的做法将提出另一种 $2^{m-|B|}$ 的做法，我们通过数据分治可以将复杂度降低到 $O(2^{\frac{m}{2}})$。

首先我们定义以下集合幂级数 $F_A(z)$ 和普通多项式 $P_A(z)$，其中 $A$ 是一个线性基：

$$ \begin{aligned} F_A(z) = \sum_{S \in \text{span}(A)} z^{S}\\ P_A(z) = \sum_{S \in \text{span}(A)} z^{|S|} \end{aligned} $$

假设现在询问是求 $i=c$ 的答案，首先一个显然的答案是 $[z^c]P_A(z)$ 但是它看起来毫无优化空间，于是我们考虑构造集合幂级数

$$ G_c(x) = \sum_{|S|=c} z^{S} $$

那么答案就是

$$ [z^0]F_A(z)\times G_c(z) $$

这里的卷积运算定义为集合对称差卷积（也就是异或和卷积）。

这样求显然是没暴力快的，但是对于对称差卷积我们一般都考虑 FWT，先复习回顾一下 FWT 的定义：

$$ \begin{aligned} FWT(A(z)) &= \sum_{S} z^S(\sum_{T} (-1)^{S \cap T} [z^T]A(z))\\ IFWT(A(z)) &= \frac{1}{2^m} \sum_{S} z^S (\sum_{T}(-1)^{S \cap T} [z^T]A(z))\\ FWT(A(z) \times B(z)) &= FWT(A(z)) \cdot FWT(B(z)) \end{aligned} $$

那么我们可以把答案拆成

$$ [z^0]IFWT(FWT(F_A(z)) \cdot FWT(G_c(z))) $$

首先我们注意到：

$$ [z^0]IFWT(A(z)) = \frac{1}{2^m}\sum_{T} [x^T]A(z) $$

所以答案可以进一步简化成：

$$ \frac{1}{2^m} \sum_T [x^T] FWT(F_A(z)) \cdot FWT(G_c(z)) $$

我们来研究一些性质：首先我们根据线性基的性质显然会有 $x^{S} \times F_A(z) = F_A(z)(S \in \text{span}(A))$，所以我们可以得到 $F_A(z) \times F_A(z) = 2^{|A|}F_A(z)$。

所以可以得到：

$$ \begin{aligned} FWT(F_A(z) \times F_A(z)) = FWT(F_A(z)) \cdot FWT(F_A(z))\\ FWT(2^{|A|} F_A(z)) = FWT(F_A(z)) \cdot FWT(F_A(z)) \end{aligned} $$

我们任取 $FWT(F_A(z))$ 某一项系数 $x$，可以得到 $2^{|A|}x = x^2$，解得 $x_1=0,x_2=2^{|A|}$。

然后我们回归 $FWT(F_A(z))$ 的定义：

$$ [z^S]FWT(F_A(z)) = \sum_{T} (-1)^{|S \cap T|} \in \{0,2^{|A|}\} $$

所以我们发现 $[z^S]FWT(F_A(z))=2^{|A|}$ 的充要条件为 $\forall T \in \text{span}(A),(-1)^{|S| \cap |T|} = 1$。

我们定义线性基 $A$ 的正交基 $B$ 为：$\forall x \in \text{span}(A),y \in \text{span} (B),(-1)^{|x \cap y|} = 1$ 且 $\text{rank}(A)+\text{rank}(B) = m$。一种构造方法是首先用高斯-约旦消元法把主元列其他地方都消成 0 ，然后将线性基转置后交换主元和自由元 ，如下图所示：

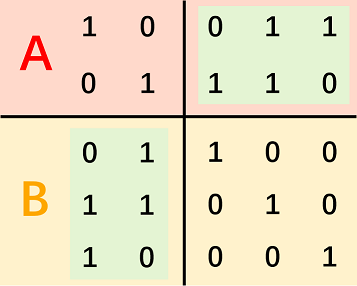
证明：首先我们要发现 $|x \cap y|$ 的奇偶性对异或是有结合律的（可以枚举证明），所以我们只要求基两两满足条件即可。以上构造就可以满足条件（我也不知道怎么想到的，但是验证确实是满足条件的一组基）

于是我们可以发现：

$$ FWT(F_A(z)) = F_B(z)\cdot 2^{|A|} $$

代入原式可得

$$ \frac{1}{2^m} \sum_S [z^S] F_B(z) \cdot 2^{|A|} \cdot FWT(G_c(z)) $$

可以发现 $\text{rank}(B) = m-\text{rank}(A)$，所以可以爆搜 $\text{span}(B)$，然后我们考虑去枚举集合 $S$ 的大小：

$$ \frac{1}{2^{m-|A|}} \sum_{x \geq 0} [z^x]P_B(z)\cdot \sum_{|S|=x}[z^S]FWT(G_c(z)) $$

首先可以发现

$$ [z^S]FWT(G_c(z)) =\sum_{T} (-1)^{S \cap T} [|T|=c] $$

所以我们考虑去枚举 $S \cap T$ 的大小 $i$，考虑组合意义可以得到

$$ \frac{1}{2^{m-|A|}} \sum_{x \geq 0} [z^x]P_B(z)\cdot \sum_{i \geq 0}(-1)^i \binom x i \binom{m-x}{c-i} $$

就可以计算出 $i=c$ 的答案了。

时间复杂度是 $O(2^{\frac{m}{2}} + m^3)$。可以通过 E2。

但是注意到我们爆搜的部分还是可以用折半搜索+FWT优化的，所以时间复杂度实际可以优化到 $O(2^{\frac{m}{4}}\times m+m^3)$ 的吧..?看看以后有没有毒瘤出题人出了。

好题啊，以后看到集合幂级数快速算对称差卷积就去考虑一下 FWT 的意义吧。

F

代码写不动了，于是就说说思路吧：

我们只需要分类讨论几种情况就可以了。

1. LCA不同的情况

我们考虑在LCA深度较浅的地方统计。我们发现如果两个链有交那么其中一个的lca必定在另一条链上，也就是这个lca在另一条链上延伸某个长度。于是我们枚举lca，对于某个链 $(u,v)$，我们先查询一下点 $u$ 和点 $v$ 的值，然后对 $lca$ 往 $u$ 和 $v$ 的方向往下 $k$ 步的点的子树做一个子树加。树状数组就可以完成了。

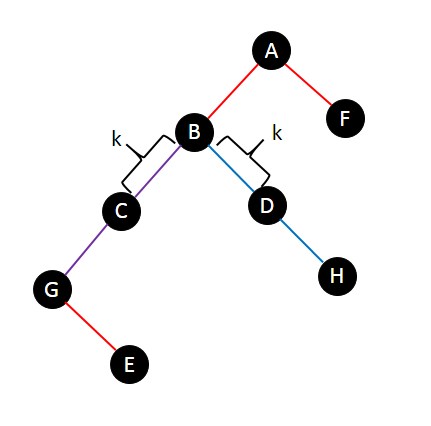
两条链分别是 $G - H$ 和 $E - F$。这个图里我们就要在 $B$ 的位置给 $C$ 和 $D$ 子树加（$dis(B,C)=dis(C,D)=k$），然后在 $A$ 的时候查询点 $E,F$ 的值。

2. LCA 不同的情况

我们先对于一条链，设 $dfn_u < dfn_v$。

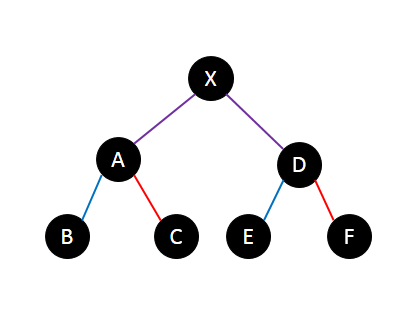
两条链 $B-D$ 和 $C-F$，其中 $dfn_B < dfn_D,dfn_C < dfn_F$。

那么我们发现我们找到 $B,D$ 的 lca $A$，然后把 $A$ 向 $C$ 方向跳 $k$ 步，走到的店的子树内每一个点都满足条件。

但是每次这样暴力肯定人就没了，所以我们对于每个lca，以所有链的 $u$ 点建虚树，启发式合并只需要考虑插入一个新点的贡献就行了，而贡献显然可以用线段树轻松维护。

3. 一种遗漏的情况

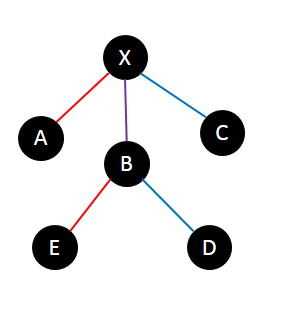
两条链分别是 $A-E$ 和 $C-D$，其中 $dfn_A < dfn_E < dfn_D < dfn_C$，发现这样你找到 $lca(A,D)=X$ 之后就不知道向哪里走了，也就是说交是从 $lca$ 往下的一条链这种情况我们漏掉了。

对于这种问题我们可以把链按照 $dfn_u$ 排序，交就是从 $X$ 往下的一条链，就可以在往下 $k$ 步的地方子树查询了（类似情况 $1$）

所以这题复杂度估计是 $O(n\log^2 n)$ 级别的，大致流程就是对于每个lca，建立虚树，在虚树上启发式合并，over。