感觉没有 ytq 哥哥之前的毒瘤画风了,很怪异。
做的时候一直以为我做法假了爆零了,结果发现并不是这样?不过还是垫底了
A
考场做法:
我们肯定贪心从小往大选,所以先按照 $a_i$ 排序。
可以看成每个时间 $i$ 种钻石补充了 $b_i$ 个,我们肯定贪心从小往大选,我们每次需要找到第一个位置满足前缀和 $\geq c_i$,然后选这前面的宝石。可以用线段树维护一次函数和完成。
还有一个做法:我们设 $c$ 的前缀和是 $sm_i$,那么求 $(i,sm_i)$ 的凸包,对于每条边对应的区间我们都买数量一样的宝石。正确性就是可以通过调整变得更好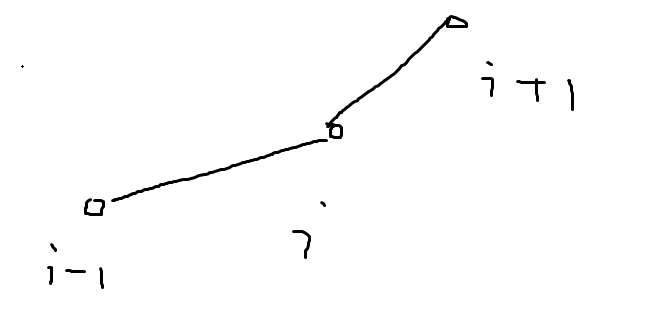
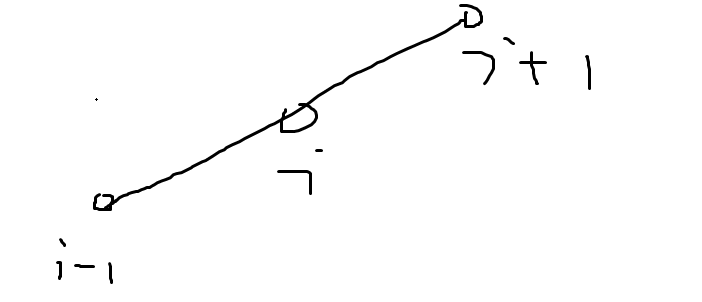
图一如果满足限制,图二一定也满足限制,并且注意到代价函数下凸,所以图二的代价一定比图一的小。我们就证明了要求凸包。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 2e5 + 5;
LL sm1[MAXN<<2],sm2[MAXN<<2],coe1[MAXN<<2],coe2[MAXN<<2];
LL tag[MAXN<<2],clr[MAXN<<2];
LL c[MAXN];
P a[MAXN];
int n,m;
#define lc ((x)<<1)
#define rc ((x)<<1|1)
inline void pushup(int x){
sm1[x] = sm1[lc]+sm1[rc];
sm2[x] = sm2[lc]+sm2[rc];
coe1[x] = coe1[lc]+coe1[rc];
coe2[x] = coe2[lc]+coe2[rc];
}
inline void build(int x,int l,int r){
if(l == r){
sm1[x] = sm2[x] = 0;
coe1[x] = a[l].se;coe2[x] = 1ll*a[l].fi*a[l].se;
return;
}
int mid = (l + r) >> 1;
build(lc,l,mid);build(rc,mid+1,r);
pushup(x);
}
inline void cover(int x,LL d){
sm1[x] += coe1[x]*d;
sm2[x] += coe2[x]*d;
tag[x] += d;
}
inline void reset(int x){
sm1[x] = sm2[x] = tag[x] = 0;clr[x] = 1;
}
inline void pushdown(int x){
if(clr[x]){
reset(lc);
reset(rc);
clr[x] = 0;
}
if(tag[x]){
cover(lc,tag[x]);
cover(rc,tag[x]);
tag[x] = 0;
}
}
inline void modify(int x,int l,int r,int L,int R){
if(L > R) return;
if(l == L && r == R){
reset(x);
return;
}
int mid = (l + r) >> 1;pushdown(x);
if(R <= mid) modify(lc,l,mid,L,R);
else if(L > mid) modify(rc,mid+1,r,L,R);
else modify(lc,l,mid,L,mid),modify(rc,mid+1,r,mid+1,R);
pushup(x);
}
inline LL query1(int x,int l,int r,int L,int R){
if(L > R) return 0;
if(l == L && r == R) return sm1[x];
int mid = (l + r) >> 1;pushdown(x);
if(R <= mid) return query1(lc,l,mid,L,R);
if(L > mid) return query1(rc,mid+1,r,L,R);
return query1(lc,l,mid,L,mid)+query1(rc,mid+1,r,mid+1,R);
}
inline LL query2(int x,int l,int r,int L,int R){
if(L > R) return 0;
if(l == L && r == R) return sm2[x];
int mid = (l + r) >> 1;pushdown(x);
if(R <= mid) return query2(lc,l,mid,L,R);
if(L > mid) return query2(rc,mid+1,r,L,R);
return query2(lc,l,mid,L,mid)+query2(rc,mid+1,r,mid+1,R);
}
inline int getpos(int x,int l,int r,int k){
if(l == r) return l;
int mid = (l + r) >> 1;
pushdown(x);
LL ls = sm1[lc];
if(k <= ls) return getpos(lc,l,mid,k);
else return getpos(rc,mid+1,r,k-ls);
}
inline void update(int x,int l,int r,int p,int d){
if(l == r){
sm1[x] += d;
sm2[x] += 1ll*d*a[l].fi;
return;
}
pushdown(x);
int mid = (l + r) >> 1;
if(p <= mid) update(lc,l,mid,p,d);
else update(rc,mid+1,r,p,d);
pushup(x);
}
int main(){
scanf("%d%d",&m,&n);
FOR(i,1,m) scanf("%d",c+i);
FOR(i,1,n) scanf("%d%d",&a[i].fi,&a[i].se);
std::sort(a+1,a+n+1);n = 1;
while(a[n].se != -1) ++n;
if(n == 1){
LL ans = 0;
FOR(i,1,m) ans += 1ll*c[i]*a[1].fi;
printf("%lld\n",ans);
return 0;
}
int N = n-1;build(1,1,N);
LL ans = 0;
FOR(i,1,m){
pushdown(1);cover(1,1);
if(sm1[1] <= c[i]){
ans += 1ll*(c[i]-sm1[1])*a[n].fi;
ans += sm2[1];
reset(1);
}
else{
int p = getpos(1,1,N,c[i]);
LL r = c[i]-query1(1,1,N,1,p-1);
ans += 1ll*query2(1,1,N,1,p-1)+1ll*r*a[p].fi;
modify(1,1,N,1,p-1);
update(1,1,N,p,-r);
}
}
printf("%lld\n",ans);
return 0;
}B
排序代码写成
inline bool cmp(std::string a,std::string b){
return a+b < b+a;
}感觉是经典题了。
这里注意尽量不要用字符串加法(当然这个cmp可以,但是输出的时候不要用加号)
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 3e5 + 5;
std::string s[MAXN];
inline bool cmp(std::string a,std::string b){
return a+b < b+a;
}
int main(){
std::ios::sync_with_stdio(false);
int n;std::cin >> n;
FOR(i,1,n) std::cin >> s[i];
std::sort(s+1,s+n+1,cmp);
FOR(i,1,n) std::cout << s[i];
std::cout << '\n';
return 0;
}C
如果不考虑后手能选择一个集合,其实就是一个 K-Nim 游戏:
K-Nim 游戏:每次可以选择 $k$ 堆,拿走任意个数的石子,无法操作者输
结论:石子数二进制每一位的和如果都 $\bmod k+1=0$,那么先手必败,否则先手必胜。
我们先证明必败态操作一步一定回到必胜态:
首先显然至少有一位的 $1$ 个数变动了。最多操作 $k$ 个,每一位的 $1$ 的个数变动不会超过 $k$,一定不会是 $k+1$ 的倍数。
再证明必胜态一定有一种操作到必败态:
我们从高到低考虑所有为,假设存在一种方法改变了 $m$ 堆,使 $i$ 之前的所有位回到了 $k+1$ 的整数倍,现在要证明有一种方法让第 $i$ 位也恢复到 $k+1$ 整数倍。
首先发现对于已经被改变的 $m$ 堆在第 $i$ 位可以自由选择。
设除去已经更改的 $m$ 堆,剩下堆 $i$ 位上的 $1$ 的个数位 $sum$。
- $sum \leq k-m$,把剩下堆是 $1$ 的全变成 $0$ 即可,还是满足选取个数的
- $sum > k-m$,在之前改变的 $m$ 堆选择 $k+1-sum$ 堆设置成 $1$,其余设置成 $0$。发现 $k+1-sum < k+1-(k-m) < m+1$,$k+1-sum \leq m$,可以达到。
那么加上后手可以选择一个集合就是要求不存在一个非空子集,三进制不进位加法结果 $=0$。
我们发现每次加入两个这个限制就像是强行拼凑的一样,考虑三进制加法下 $2x=-x$。所以我们就可以去考虑线性基了(因为一个线性组合所需的所有系数我们都可以造出来了)
所以必胜等价于这些数字在三进制不进位加法下线性无关。就可以用线性基维护了(每次如果插入的权值大于这个地方的权值就交换接着下去消)
为了加快速度需要位运算优化,看一下代码理解就行了(其实本质就是把所有可能这一位是 1 的情况都写出来 )
(所以这个题是不是可以加强到 $k$ 进制啊)
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
struct Node{
LL v[2];
Node(LL x=0,LL y=0){
v[0] = x;v[1] = y;
}
inline LL& operator [] (const int &n){return v[n];}
friend Node operator + (Node x,Node y){
return Node(
(x[1]&y[1])|(x[0]&(~(y[0]|y[1])))|(y[0]&(~(x[0]|x[1]))),
(x[0]&y[0])|(x[1]&(~(y[0]|y[1])))|(y[1]&(~(x[0]|x[1])))
);
}
}b[60];
LL y[60],sm;
inline void insert(Node x,LL v){
ROF(i,59,0){
if(((x[0]|x[1])>>i)&1){
if(!(((b[i][0]|b[i][1])>>i)&1)){
b[i] = x;y[i] = v;sm += v;return;
}
if(v > y[i]) sm += v-y[i],std::swap(v,y[i]),std::swap(x,b[i]);
if(MP((x[0]>>i)&1,(x[1]>>i)&1) == MP((b[i][0]>>i)&1,(b[i][1]>>i)&1)){
x = x+b[i]+b[i];
}
else{
x = x+b[i];
}
}
}
}
int main(){
int n;scanf("%d",&n);
FOR(i,1,n){
LL x,y;scanf("%lld%lld",&x,&y);
x ^= sm;
insert(Node(x,0),y);
printf("%lld\n",sm);
}
return 0;
}