A

显然深度相同的点会一起到达一号点，只需要求出深度然后取模加起来即可。

B

我们先暴力把所有可能的串都求出来，然后我们按照第一个字符进行分类。

对于每一类，我们暴力枚举询问哪一位，计算出来询问这一位能区分出这一类中的几个，取个最大值作为这一类的答案。最终的答案是每一类的答案的和。

C

设 $a_i$ 表示覆盖点 $i$ 个区间个数，我们画图发现所有满足存在一个点被所有区间覆盖等价于 $a$ 是单峰的（不严格，中间可以相等）。

所以我们相当于要找一个最长单峰子序列。直接树状数组优化 dp 处理出以 $i$ 开头/结尾的最长下降/上升子序列就好了。

D

我们先考虑如何去检验某个点是否可行：只需要看它四个方向是否有黑色棋子能拦住它就行了。

所以这启发我们研究黑色棋子能拦住哪些位置的白色棋子，我们把黑色棋子当原点，不难发现：

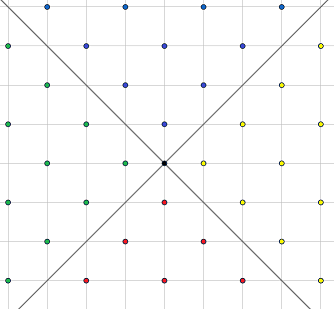
能拦住和它曼哈顿距离是奇数的棋子，并且每个黑色棋子只能选择一个方向去拦截。

证明：发现如果曼哈顿距离是偶数的时候一定能达到某种局面满足黑色棋子和白色棋子挨着并且轮到黑色棋子移动，白色棋子就可以溜了。。

那么我们考虑旋转坐标系，现在变成了：

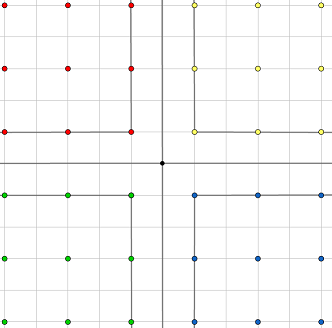
首先可以把黑色点按照坐标和的奇偶性分类，两种棋子能阻挡的白色棋子一定互不相交，然后把点坐标都除二，我们发现所有黑色棋子都在整数点上，而所有满足条件的白色棋子都在形如 $(x+0.5,y+0.5)$ 的点上，就不用去考虑奇偶分类讨论哪些点可以选哪些不能选了。

然后我们就可以去枚举白色点的 $y$ 坐标，从上下两边分别找出 $x$ 坐标最小值和最大值，区间交然后找区间内形如 $(x+0.5,y+0.5)$ 的点的个数即可。实际上你可以不除二但是需要讨论交的端点的奇偶性，比较麻烦。

E

就差了一步离散化没想好。。

首先一个暴力的 dp 是 $f_{i,j,k}$ 表示考虑了前 $i$ 个数，所有右端点 $\leq i$ 的限制都被满足，最后一个 $0$ 在位置 $j$，最后一个 $1$ 在位置 $k$ 的方案数，转移枚举下一个填 $0/1$ 就好了。

我们发现有一维是和 $i$ 相等的，所以我们可以压缩状态：设 $f_{i,j,0/1}$ 表示考虑前 $i$ 位，第 $i$ 位填的是 $0/1$，并且上一个和当前位置不同的数字的位置是 $j$ 的方案数，但是由于值域太大了根本优化不下去。我们可以考虑离散化。

首先观察一些性质：所有没有线段右端点的位置的转移都是十分类似的，所以我们只需要关心右端点的位置；发现如果一个位置满足 $x,x+1$ 都不是左端点的话，那么我们无需关心谁是最后一个 $0$（因为在限制上体现都是一样的）

所以我们把区间写成左开右闭区间，然后对着离散化一下，设离散化后排名 $i$ 的数的的真实位置是 $x_i$，可以设 $f_{i,j,0/1}$ 表示考虑前 $i$ 个数，第 $i$ 个位置填的是 $0/1$，第一个和这个不相同的位置是 $\in (x_{j-1},x_j]$。

我们预处理个 $lim_{0/1,i}$ 表示属性 $0/1$ 的限制，所有右端点 $\leq i$ 的左端点最紧的那个，写一下 dp 转移：

$$ \begin{aligned} f_{i,j,0} &\to f_{i+1,j,0}\\ f_{i,j,0} &\to f_{i+1,i,1}\\ f_{i,j,0} &\times (2^{x_{i+1}-x_i-1}-1) \to f_{i+1,i+1,0},f_{i+1,i+1,1} \end{aligned} $$

用 $lim_{0/1}$ 判断一下状态是否合法就行了。
运用 CF1327F 中 F 题的方法就可以优化 dp 到 $O((n+m)\log k)$，以下是题解：

注意这里一定要写成左开右闭区间，因为设一个左端点为 $x$，我们却只关心是否有 $j < x$ 也就是 $j \leq x-1$，所以要保证每个点代表的区间都全部是合法/不合法的，不能混在一起。这也提醒了我们离散化 dp 的时候要看每一维需要什么，并且要求每个区间的性质必须完全相同，而不是想当然看到区间就离散化左右端点。