A

我们固定 $s$ ，循环位移所有 $t$，发现答案就是相同的字母对数。

而循环位移 $s$ 是本质不变的，所以答案乘个 $n$ 就好了。

所以你构造的串中每个字母都要保证是 $s$ 中出现次数最大的，设这样的字母有 $c$ 个，答案显然是 $n^c$。

B

从高到低位贪心一定是最优的。

对于每个点，我们可以通过判断周围点是否存在来确定这个点是否可以取走，每次取走能取的最大/最小后更新周围的点即可。

C

考虑每个数的贡献。枚举这个数下一个加号在哪里（我们这里没有计算 $j=n$ 的情况，因为可以 $O(n)$ 简单计算。）

$$ \begin{aligned} &\sum_{i=1}^n a_i\sum_{j=i}^{n-1} 10^{j-i}\binom{n-j+i-2}{k-1}\\ &= \sum_{i=1}^n \frac{a_i}{10^i}\sum_{j=0}^{n-1-i} \binom{n-j-2}{k-1} 10^{j+i}\\ &= \sum_{i=1}^n a_i\sum_{j=0}^{n-i-1}\binom {n-j-2}{k-1}10^j \end{aligned} $$

处理 $\sum_{i=0}^x \binom {n-x-2}{k-1}10^j$。

D

一定是先赋值，再加法，再乘法。考虑将所有操作都转化为乘法，然后贪心即可。

E

观察一下三条不交路径，一定形成了两个相交的环。

对于这种问题我们考虑它的反面：如果不存在解一定是不存在两个相交的环，也就是每一个边至多出现于一个环上，也就是个边仙人掌。

判断边仙人掌可以树上差分，然后只需要按照构造找出来一对路径 $(u_1,v_1)$ 和 $(u_2,v_2)$ 满足有交，设 $dep_{u_1} < dep_{v_1},dep_{u_2} < dep_{v_2}$，如下图：

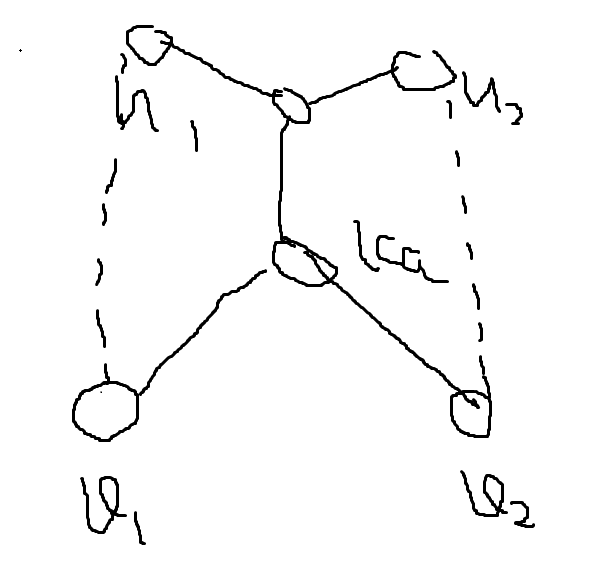
其中 $lca = lca(v_1,v_2)$，设那个没有标记的点是 $x$，我们可以构造三条 $\text{lca} \to x$ 的路径：分别是 $\text{lca} \to x$；$\text{lca} \to v_1 \to u_1 \to x$；$\text{lca} \to v_2 \to u_2 \to x$。