A
对点权取 $\ln$ 变成加法就行了。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 2e5 + 5;
const int ha = 1e9 + 7;
std::vector<int> G[MAXN];
int n,a[MAXN];
long double f[MAXN][2];
inline void dfs(int v,int fa=0){
long double val = logl((long double)a[v]);
f[v][1] = val;f[v][0] = 0;
for(auto x:G[v]){
if(x == fa) continue;
dfs(x,v);
if(f[x][1] > f[x][0]) f[v][0] += f[x][1];
else f[v][0] += f[x][0];
f[v][1] += f[x][0];
}
}
int ans = 1;
inline void dfs2(int v,int las=0,int fa=0){
bool flag = 0;
if(!las){
long double val = logl((long double)a[v]);
long double w1 = 0,w2 = val;
for(auto x:G[v]){
if(x == fa) continue;
if(f[x][1] > f[x][0]) w1 += f[x][1];
else w1 += f[x][0];
w2 += f[x][0];
}
if(w1 < w2) ans = 1ll*ans*a[v]%ha,flag = 1;
}
for(auto x:G[v]){
if(x == fa) continue;
dfs2(x,flag,v);
}
}
int main(){
scanf("%d",&n);
FOR(i,1,n) scanf("%d",a+i);
FOR(i,2,n){
int u,v;scanf("%d%d",&u,&v);
G[u].pb(v);G[v].pb(u);
}
dfs(1);dfs2(1);
printf("%d\n",ans);
return 0;
}B
我们连边 $(x,2x)$,发现图形如若干链,链头都是一个不包含质因子 $2$ 的数字,设链头数字为 $x$,长度为 $l$,需要满足 $x2^{l-1} \leq n$。
发现本质不同的长度只有 $\log n$ 种,算出来每种长度的数量(这里我用的是容斥),对于偶数长度每个集合获得的长度是一样的,方案数是 $2$。对于奇数长度有一个集合会获得更多的一个,我们可以解出要选多少个奇数集合,lucas 定理即可。
其实发现每次组合数上面数是不变的,而下降幂最多过 $\text{mod}$ 次就会变成 $0$。。。预处理最后几项就行。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<LL,LL>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int ha = 10000019;
const int MAXN = 1e5 + 5;
LL cnt[114];
inline int qpow(int a,LL n=ha-2){
int res = 1;n %= (ha-1);
while(n){
if(n & 1) res = 1ll*res*a%ha;
a = 1ll*a*a%ha;
n >>= 1;
}
return res;
}
int fac[ha],inv[ha];
inline int C(LL n,LL m){
if(n < 0 || m < 0 || n < m) return 0;
if(n < ha && m < ha) return 1ll*fac[n]*inv[m]%ha*inv[n-m]%ha;
else return 1ll*C(n%ha,m%ha)*C(n/ha,m/ha)%ha;
}
inline void prework(){
fac[0] = 1;
FOR(i,1,ha-1) fac[i] = 1ll*fac[i-1]*i%ha;
inv[ha-1] = qpow(fac[ha-1]);
ROF(i,ha-2,0) inv[i] = 1ll*inv[i+1]*(i+1)%ha;
}
int main(){
prework();
LL n;int q;scanf("%lld%d",&n,&q);
FOR(i,0,60){
LL t = n/(1ll<<i);
if(!t) break;
if(t&1) cnt[i+1]++,t--;
cnt[i+1] += t/2;
}
int lg = 0;LL x = n;
while(x) x >>= 1,lg++;
FOR(i,1,60) cnt[i] -= cnt[i+1];
LL now = 0,s2 = 0;int B = 1;
FOR(i,0,lg){
if(!cnt[i]) continue;
if(i&1){
int t = i/2;
now += cnt[i]*t;
s2 += cnt[i];
}
else{
now += cnt[i]*i/2;
B = 1ll*B*qpow(2,cnt[i])%ha;
}
}
while(q--){
LL m = 0;
int ans = B;
scanf("%lld",&m);
if(now > m){
puts("0");
}
else{
LL r = m-now;
ans = 1ll*ans*C(s2,r)%ha;
printf("%d\n",ans);
}
}
return 0;
}C
相当于是问所有数 $\geq x$ 的划分数。
我们考虑划分数的两个dp:
设 $f_{i,j}$ 表示考虑了 $1\ldots i$ 里的数,和为 $j$ 的方案数,每次是做一个完全背包。
设 $g_{i,j}$ 表示选了 $i$ 个数和为 $j$ 的方案数,转移枚举整体加一或者是放进去一个 $1$,$g_{i,j} = g_{i,j-i}+g_{i-1,j}$。
我们考虑根号分治,将所有数按照与 $\sqrt{n}$ 的大小关系分类。对于 $\leq \sqrt{n}$ 的数就直接跑 $f$,也就是说 $f$ 的第一维只需要 $\leq \sqrt{n}$,复杂度 $O(n\sqrt{n})$。
对于 $>\sqrt{n}$ 的数,只会选 $<\sqrt{n}$ 个,跑 $g$,复杂度 $O(n \sqrt {n})$。
总复杂度:$O(n\sqrt n)$。
考试的时候差点想出来。。。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 1e5 + 5;
int x,y,n,ha;
inline void add(int &x,int y){
x += y;if(x >= ha) x -= ha;
}
int f[MAXN],g[MAXN],h[MAXN];
/*
f[i][j]: 考虑了前i个数 和为j
g[i][j]: 选了i个数 和为j
g[i][j] = g[i-1][j]+g[i-1][j-i]
g 只考虑所有>B的数 将所有数字最后加个B+1
g[i][j] = g[i-1][j]+g[i][j-i]
所以 i<=n/B
*/
inline int solve(int x){// >= x
if(x > n) return 0;
int B = std::sqrt(1.0*n);
B = std::max(B,x-1);
CLR(f,0);CLR(g,0);CLR(h,0);
f[0] = 1;FOR(i,x,B) FOR(j,0,n) if(j >= i) add(f[j],f[j-i]);
g[0] = 1;h[0] = 1;
FOR(i,1,n/B){
FOR(j,0,n){
if(j >= i) add(g[j],g[j-i]);
if(j+i*(B+1) <= n) add(h[j+i*(B+1)],g[j]);
}
}
int ans = 0;
FOR(i,0,n) add(ans,1ll*f[i]*h[n-i]%ha);
return ans;
}
int main(){
scanf("%d%d%d%d",&x,&y,&n,&ha);
int t1 = solve(x),t2 = solve(y+1);
int ans = t1;add(ans,ha-t2);
printf("%d\n",ans);
return 0;
}D
第一步都没观察到。。。。
首先我们将原串做一些处理:如果开头和结尾的字符都是相同的,同时删除两个字符。这样我们发现 $A$ 或者 $E$ 一定有一个消失了。于是转化为对剩下的串划分,使得 $A+C$ 或 $B+D$ 是回文串。
我们先考虑 $A+C$ 怎么做,$B+D$ 只需要反过来做一遍就行了。
我们先枚举回文中心在哪个位置,分类讨论一下:
首先我们肯定是希望回文长度尽量长的,要不然损失两个才多获得一个不划算。
- 回文中心在 $A$

枚举一下回文中心,实际上是要判断后面是否有串和红色不交,并且是黄色串的倒序。我们将这个串翻转拼接在后面,就是问是否存在一个位置,他的 border。这个我们只需要求出每个前缀对应的后缀,border 集合包含它的最靠后的位置就行了。这个东西可以先更新一下最长 border,然后因为 border 的border 也能被这个位置更新,倒着扫一遍就行了。
- 回文中心在 $C$
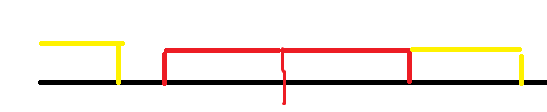
最终的方案一定是形如这样的,红色是一个回文串。我们要求出每个后缀,他能扩展到的最远位置,满足他是前缀的逆序。这个也可以把反串接到后面,然后直接用 kmp 的 next 数组更新就行了。
这里可能会有疑惑:如果黄色和红色有交了怎么办?本来是要暴力跳 next 的,但是发现:
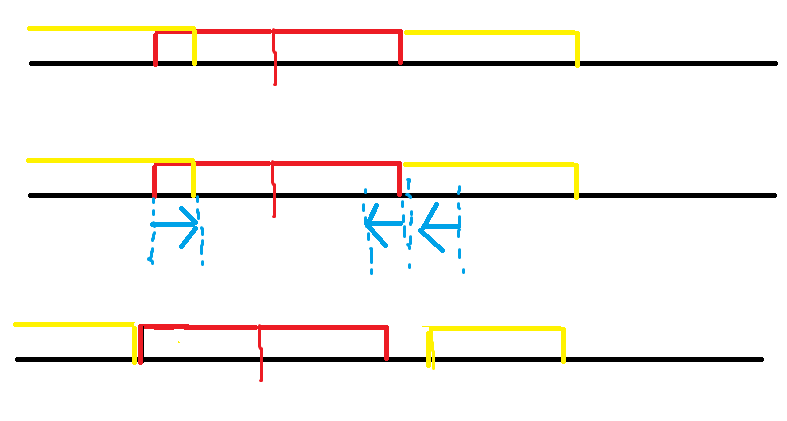
箭头指向的方向表示这个串的顺序或逆序,这三个串是相同的。
我们可以认为算了第三种方案,所以直接和长度取 $\min$ 即可。
当然如果你直接 exkmp 就没那么麻烦了,上面的操作都是要求一个后缀和一个串的 lcs。
细节有点多,要分开讨论奇回文后缀和偶回文后缀。。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 1e7 + 5;
char str[MAXN];
int n,ans = 0;
int r[MAXN];
char s[MAXN],ss[MAXN];
inline void manacher(int n){
int N = 0;s[0] = '$';
s[N = 1] = '#';FOR(i,1,n) s[++N] = str[i],s[++N] = '#';
int mid = 0;
FOR(i,1,N){
if(i <= mid+r[mid]) r[i] = std::min(r[2*mid-i],mid+r[mid]-i);
else r[i] = 1;
while(s[i+r[i]] == s[i-r[i]]) ++r[i];
if(i+r[i] > mid+r[mid]){
mid = i;
}
}
}
int g[MAXN];
// 后缀i能和反串的后缀匹配到哪里
int h[MAXN];
// 前缀i的逆最靠后可以匹配到哪个位置
int nxt[MAXN];
inline void work(int n){
CLR(nxt,0);CLR(g,0);CLR(s,0);CLR(ss,0);CLR(r,0);CLR(h,0);
manacher(n);
int nn = 0;
FOR(i,1,n) ss[++nn] = str[i];
ss[++nn] = '$';
ROF(i,n,1) ss[++nn] = str[i];
std::reverse(ss+1,ss+nn+1);
int j = 0;
FOR(i,2,nn){
while(j && ss[i] != ss[j+1]) j = nxt[j];
if(ss[i] == ss[j+1]) ++j;
nxt[i] = j;
}
FOR(i,n+2,nn) h[nxt[i]] = std::max(h[nxt[i]],n-(i-n-1)+1);
ROF(i,n,1) h[nxt[i]] = std::max(h[nxt[i]],h[i]);
std::reverse(nxt+1,nxt+nn+1);
FOR(i,1,n) g[i] = nxt[i];
FOR(i,1,2*n) ans = std::max(ans,r[i]-1);
FOR(i,1,n){ // i处的奇回文
int l = r[2*i]/2;
ans = std::max(ans,r[2*i]-1+2*std::min(g[i+l],i-l));
if(h[i-l] >= i+l) ans = std::max(ans,r[2*i]-1+2*(i-l));
}
FOR(i,1,n-1){ // (i,i+1)处的偶回文
int l = (r[2*i+1]-1)/2;
ans = std::max(ans,r[2*i+1]-1+2*std::min(g[i+l+1],i-l));
if(h[i-l] >= i+l+1) ans = std::max(ans,r[2*i+1]-1+2*(i-l));
}
}
int main(){
scanf("%s",str+1);n = strlen(str+1);
int l = 1,r = n;
while(l <= r && str[l] == str[r]) l++,r--;
if(l > r){
printf("%d\n",n);
exit(0);
}
int gx = l-1;
int t = 0;
FOR(i,l,r) str[++t] = str[i];
FOR(i,t+1,n) str[i] = 0;
work(t);
std::reverse(str+1,str+t+1);
work(t);
ans += gx*2;
printf("%d\n",ans);
return 0;
}