A
我考试的做法是贪心:首先这个题目等价于要求回到根(可以传送),那么如果没有传送操作,答案就是按照 $dfn$ 序走,有了传送只需要在每一步判下是传送回去再走过来优还是直接走优了。注意这样我们要先遍历深度最大值比较小的点,这样就能在最后传送回去,不会浪费。
题解的做法是dp。对于这种树上游走的题目我们可以设 $f_{v,0}$ 表示从 $v$ 出发,走完子树,不用回到 $v$ 的代价。$f_{v,1}$ 表示从 $v$ 出发,走完子树,必须回到 $v$ 的代价。
转移考虑合并 $u$ 和儿子 $v$,有:
$$ \begin{aligned} f'_{u,0} = \min(f_{u,0}+dep_u+1+f_{v,0},f_{u,0}+f_{v,1}+2,f_{u,1}+f_{v,0}+1)\\ f'_{u,1} = \min(f_{u,1}+f_{v,0}+1+dep_u,f_{u,0}+dep_v+2+f_{v,1},f_{u,1}+f_{v,1}+2) \end{aligned} $$
就是枚举一下讨论即可。注意这里求 lca 可以暴力求,复杂度均摊 $O(n)$。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 1e6 + 5;
std::vector<int> G[MAXN];
int n,id[MAXN],dep[MAXN],f[MAXN],mx[MAXN];
inline void dfs1(int v,int fa=0){
f[v] = fa;
for(auto x:G[v]){
if(x == fa) continue;
dep[x] = dep[v]+1;dfs1(x,v);
mx[v] = std::max(mx[v],mx[x]);
}
mx[v] = std::max(mx[v],dep[v]);
}
inline bool cmp(int x,int y){
return mx[x] < mx[y];
}
inline void dfs2(int v,int fa=0){
static int ts = 0;id[++ts] = v;
std::sort(all(G[v]),cmp);
for(auto x:G[v]){
if(x == fa) continue;
dfs2(x,v);
}
}
inline int lca(int x,int y){
while(x != y){
if(dep[x] < dep[y]) std::swap(x,y);
x = f[x];
}
return x;
}
int main(){
scanf("%d",&n);
FOR(i,2,n){
int f;scanf("%d",&f);G[f].pb(i);
}
dfs1(1);dfs2(1);LL ans = 0;
FOR(i,2,n){
ans += std::min(dep[id[i]],dep[id[i-1]]+dep[id[i]]-2*dep[lca(id[i-1],id[i])]);
// printf("%d %d\n",id[i],ans);
}
printf("%lld\n",ans);
return 0;
}B
这种概率随着局面而变化的问题要考虑局面是否概率均等。
我们先设一个结束局面为 $a_1,a_2,\ldots,a_n$,求一下概率:
$$ \frac{\prod (a_i-1)!}{n^{\overline m}} \frac{m!}{\prod (a_i-1)!} = \frac{1}{\binom {n+m-1}{m}} $$
所以所有局面的概率都是相等的,我们只需要对于每一种局面,求出前 $k$ 大的和,累加起来就是答案。
为了方便,我们默认所有值从 $0$ 开始(最后自己加上就行了)
我们考虑一下第 $k$ 大的本质意义:
$$ \begin{aligned} kth &= \sum_{i=1}^{n} [i=kth]i\\ &= \sum_{i=1}^n [i \leq kth]\\ &= \sum_{i=1}^n [\text{有至少 i 个数字} \geq kth] \end{aligned} $$
所以我们考虑对这个求和。我们设 $f_{i,j}$ 表示有至少 $i$ 个数字 $\geq j$ 的集合的个数,设一次询问为 $r$,答案就是
$$ \sum_{i=1}^r \sum_{j=1}^n f_{i,j} $$
我们可能会想到一个很 naive 的式子:我们选出 $i$ 个数字,强制 $\geq j$,剩下的操作随便分配,也就是
$$ \binom{n}{i}\binom{m-ij+n-1}{n-1} $$
但是我们发现这样会多算:每个有 $x$ 个 $\geq j$ 的数字的集合会被算 $\binom x i$ 次!不过这样的重复系数让我们想到了二项式反演。
设 $g_{i,j}$ 表示恰好有 $i$ 个数字 $\geq j$ 的集合的个数,根据上面的分析显然有:
$$ \begin{aligned} & \binom n i \binom{m-ij+n-1}{n-1} = \sum_{k=i}^n \binom k i g_{k,j}\\ & \Rightarrow g_{i,j} = \sum_{k=i}^n (-1)^{k-i}\binom k i \binom n k \binom {m-kj+n-1}{n-1} \end{aligned} $$
我们分析一下暴力计算的复杂度是什么:显然有 $ij \leq m$,并且 $m-kj+n-1 \geq n-1 \Rightarrow jk \leq m$,所以复杂度是:
$$ \sum_{i=1}^m \sum_{j=1}^{\frac{m}{i}} \sum_{k=1}^{\frac{m}{j}}1 \leq \sum_{i=1}^m (\frac{m}{i})^2 = m^2\sum_{i=1}^m \frac{1}{i^2 }\leq 2m^2 = O(m^2) $$
所以总复杂度是 $O(m^2)$。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 1e5+5;
const int ha = 1e9 + 7;
inline void add(int &x,int y){
x += y-ha;x += x>>31&ha;
}
inline int qpow(int a,int n=ha-2){
int res = 1;if(n < 0) return 0;
while(n){
if(n & 1) res = 1ll*res*a%ha;
a = 1ll*a*a%ha;
n >>= 1;
}
return res;
}
int fac[MAXN],inv[MAXN],n,m;
inline int C(int n,int m){
if(n < 0 || m < 0 || n < m) return 0;
return 1ll*fac[n]*inv[m]%ha*inv[n-m]%ha;
}
inline void prework(){
fac[0] = 1;FOR(i,1,MAXN-1) fac[i] = 1ll*fac[i-1]*i%ha;
inv[MAXN-1] = qpow(fac[MAXN-1]);ROF(i,MAXN-2,0) inv[i] = 1ll*inv[i+1]*(i+1)%ha;
}
int f[5005][5005];
int main(){
prework();
scanf("%d%d",&n,&m);
FOR(i,1,n){
FOR(j,1,m/i){
FOR(k,i,m/j){
int gx = 1ll*C(k,i)*C(n,k)%ha*C(n+m-j*k-1,n-1)%ha;
if((k-i)&1) gx = ha-gx;
add(f[i][j],gx);
}
}
}
ROF(i,n,1) FOR(j,1,m) add(f[i][j],f[i+1][j]);
int p = C(n+m-1,n-1);p = qpow(p);
int sm = 0;
FOR(i,1,n){
FOR(j,1,m) add(sm,f[i][j]);
printf("%lld\n",(1ll*sm*p%ha+i)%ha);
}
return 0;
}C
考虑先离散化,变成若干个连续段。
考虑一个离散化后的区间对答案的贡献:设这个连续段的长度为 $x$,覆盖这个段的区间的标号从小到大排序为 $i_1,i_2,\ldots,i_m$。我们先考虑只查询区间 $[l,r]$ 的线段的并是什么,如果 $\exists j \in [1,m],i_j \in [l,r]$,那么就会对这个询问贡献 $x$。
但是这个存在不是很好处理,而我们发现排序后,出现在 $[l,r]$ 中的合法编号一定是一段连续段,所以我们对于一个询问 $[l,r]$,这个段对答案的贡献就是:
$$ x(\sum_{i=1}^m [i_j \in [l,r]] - \sum_{i=1}^{m-1} [i_j \in [l,r] \text{ and } i_{j+1} \in [l,r]]) $$
这也是一个经典套路。。这本质上是要统计连续段的个数($1$),我们转化为统计开头端点的个数。
那么现在我们形如有若干个操作 $(l,r,x)$ 表示如果某个询问 $[L,R]$ 满足 $[l,r] \subseteq [L,R]$,那么就会对区间有 $(l-L+1)(R-r+1)x$ 的贡献。拆一下式子可以发现是 $L(r-1)+R(l+1)-LR-(r-1)(l+1)$,分开维护四个的系数就行了。
但是这样的操作是最多有 $O(n^2)$ 个的!不过我们发现对于两个操作,如果 $l,r$ 相等,直接把 $x$ 加起来就可以了。
于是我们离散化后考虑扫描线,每次枚举一个连续段,并维护出覆盖这个连续段的所有线段,显然这样会导致一些操作的加入和删除,我们在加入的时候记录一下加入的时候在哪个块加入的,删除的时候就说明存在一个操作影响了从开始加入到现在的一段连续的区间。而每次只会影响 $O(1)$ 个操作,所以操作数是 $O(n \log n)$ 的。
这个问题启发我们统计区间上连续段的出现次数可以同时计算相邻的对数。。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 1e6 + 5;
const int ha = 1e9 + 7;
inline int qpow(int a,int n=ha-2){
int res = 1;
while(n){
if(n & 1) res = 1ll*res*a%ha;
a = 1ll*a*a%ha;
n >>= 1;
}
return res;
}
inline void add(int &x,int y){
x += y-ha;x += x>>31&ha;
}
int n,m;
std::vector<int> S;
P prob[MAXN];
std::vector<P> opt[MAXN],qry[MAXN]; // [r]<l,x>操作(l,r,x) 如果[l,r] \in [L,R] 那么贡献+x
std::vector<int> G[MAXN];
std::set<P> s;
struct Node{
int l,r,t;
Node(int l=0,int r=0,int t=0) : l(l),r(r),t(t) {}
inline bool operator < (const Node &t) const {
if(l != t.l) return l < t.l;
if(r != t.r) return r < t.r;
return t < t.t;
}
};
std::set<Node> oo;
inline void addopt(int l,int r,int ts){
// DEBUG(l);DEBUG(r);
oo.insert(Node(l,r,ts));
}
inline void delopt(int l,int r,int ts,int d){
// DEBUG(l);DEBUG(r);
auto p = oo.lower_bound(Node(l,r,-1e9));
int gx = ((LL)S[ts]-S[p->t]+ha)%ha;
if(d == -1) gx = ha-gx;
opt[r].pb(MP(l,gx));
oo.erase(p);
}
inline void ins(int id,int pos){
auto p = s.insert(MP(id,pos)).fi,l = p,r = p;
--l;++r;
// for(auto x:s){
// DEBUG(x.fi);DEBUG(x.se);
// }
// DEBUG(oo.size());DEBUG(l->fi);DEBUG(l->se);
// DEBUG(r->fi);DEBUG(r->se);
addopt(id,id,pos);
if(l->se >= 0) addopt(l->fi,id,pos);
if(r->se >= 0) addopt(id,r->fi,pos);
if(l->se >= 0 && r->se >= 0) delopt(l->fi,r->fi,pos,-1);
}
inline void del(int id,int pos){
auto p = s.lower_bound(MP(id,-1)),l = p,r = p;
// for(auto x:s){
// DEBUG(x.fi);DEBUG(x.se);
// }
--l;++r;
delopt(id,id,pos,1);
if(l->se >= 0) delopt(l->fi,id,pos,-1);
if(r->se >= 0) delopt(id,r->fi,pos,-1);
if(l->se >= 0 && r->se >= 0) addopt(l->fi,r->fi,pos);
s.erase(p);
}
struct BIT{
#define lowbit(x) ((x)&(-(x)))
int tree[MAXN];
inline void add(int pos,int x){
++pos;
while(pos){
::add(tree[pos],x);
pos -= lowbit(pos);
}
}
inline int query(int pos){
++pos;
int res = 0;
while(pos < MAXN){
::add(res,tree[pos]);
pos += lowbit(pos);
}
return res;
}
}bitl,bitr,bitlr,bit;
int ans[MAXN];
int ql[MAXN],qr[MAXN];
int main(){
scanf("%d%d",&n,&m);
FOR(i,1,n){
scanf("%d%d",&prob[i].fi,&prob[i].se);
S.pb(prob[i].fi);S.pb(prob[i].se);
}
std::sort(all(S));S.erase(std::unique(all(S)),S.end());
s.insert(MP(-1e9,-1e9));s.insert(MP(1e9,-1e9));
FOR(i,1,n){
prob[i].fi = std::lower_bound(all(S),prob[i].fi)-S.begin();
prob[i].se = std::lower_bound(all(S),prob[i].se)-S.begin();
G[prob[i].fi].pb(i);
G[prob[i].se].pb(-i);
}
int M = (int)S.size()-1;
FOR(i,0,M){
for(auto x:G[i]){
if(x > 0) ins(x,i);
else del(-x,i);
}
}
FOR(i,1,m){
scanf("%d%d",ql+i,qr+i);
qry[qr[i]].pb(MP(ql[i],i));
}
FOR(i,1,n){
for(auto x:opt[i]){// fi=l
int l = x.fi,r = i,coe = x.se;
bitl.add(l,1ll*(l+1)*coe%ha);
bitr.add(l,1ll*(r-1)*coe%ha);
bit.add(l,(ha-coe)%ha);
bitlr.add(l,(ha-1ll*(r-1)*(l+1)%ha*coe%ha)%ha);
}
for(auto x:qry[i]){
add(ans[x.se],1ll*bitl.query(x.fi)*i%ha);
add(ans[x.se],1ll*bitr.query(x.fi)*x.fi%ha);
add(ans[x.se],1ll*bit.query(x.fi)*x.fi%ha*i%ha);
add(ans[x.se],bitlr.query(x.fi));
}
}
FOR(i,1,m){
LL t = 1ll*(qr[i]-ql[i]+1)*(qr[i]-ql[i]+2)/2;
t %= ha;t = qpow(t);ans[i] = 1ll*ans[i]*t%ha;
printf("%d\n",ans[i]);
}
return 0;
}D
实际上只有一个参数,因为 $Sa_i+Tb_i = \frac{S}{T}a_i+b_i$。
我们考虑按照 $Sa_i+b_i$ 排序本质上是在干什么:设 $y=Sa_i+b_i$,那么有 $-Sa_i+y = b_i$,其实就是有一条斜率为 $-S$ 的直线,卡每个点,按照在 $y$ 轴上的截距排序。
那么我们先对好点求出凸包,对于某个斜率 $S$,如果经过坏点的直线和凸包相交,说明这个坏点会在两个最远的好点的中间,答案会 $+1$。
我们对于每个坏点,可以通过凸包上二分找到一些满足斜率如果在这个区间内答案就会 $+1$ 的区间,可能是形如 $(l,r)$ 或 $(-\infty,l) \cup (r,+\infty)$。对于第二种情况我们先让答案 $+1$,如果选到 $(l,r)$ 再让答案 $-1$。
相当于有若干条线段,选择一个点,价值是覆盖这个点的线段的和,要最小化代价,离散化+差分解决即可。
注意这里凸包二分如何写:
我们需要找到凸包上的两个点,满足这个点和两个点的连线与凸包无交。
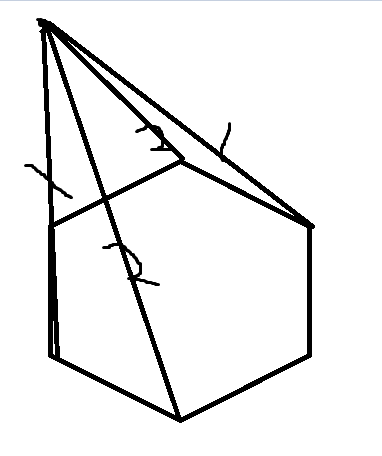
我们先找到对着这个点 $P$ 的一对边(可以通过用叉积二分解决),然后分成了两个区间,我们考虑二分一个点 $u$,考虑它顺时针下一个点 $v$,我们发现 $\vec{Pv} \times \vec{Pu}$ 在答案左边和答案右边正负号是不一样的,根据这个二分即可。
计算几何细节好多,先不写了。。
