A
考虑枚举右端点,维护所有左端点的答案:只需要处理出 $pre_i$ 表示 $i$ 前面第一个和它一样的位置,每次让 $(pre_i,i]$ 加上 $w$,$(pre_{pre_i},pre_i]$ 减去 $w$ 即可。
#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
inline char nc(){
#define SIZE 1000000+3
static char buf[SIZE],*p1 = buf+SIZE,*p2 = buf+SIZE;
if(p1 == p2){
p1 = buf;p2 = buf+fread(buf,1,SIZE,stdin);
if(p1 == p2) return -1;
}
return *p1++;
#undef SIZE
}
template <typename T>
inline void read(T &x){
x = 0;int flag = 0;char ch = nc();
while(!isdigit(ch)){
if(ch == '-') flag = 1;
ch = nc();
}
while(isdigit(ch)){
x = (x<<1) + (x<<3) + (ch^'0');
ch = nc();
}
if(flag) x = -x;
}
const int MAXN = 1e6 + 5;
LL mx[MAXN<<2],tag[MAXN<<2];
#define lc ((x)<<1)
#define rc ((x)<<1|1)
inline void cover(int x,LL d){
mx[x] += d;tag[x] += d;
}
inline void pushdown(int x){
if(tag[x]){
cover(lc,tag[x]);
cover(rc,tag[x]);
tag[x] = 0;
}
}
inline void modify(int x,int l,int r,int L,int R,int d){
if(l == L && r == R) return cover(x,d);
int mid = (l + r) >> 1;pushdown(x);
if(R <= mid) modify(lc,l,mid,L,R,d);
else if(L > mid) modify(rc,mid+1,r,L,R,d);
else modify(lc,l,mid,L,mid,d),modify(rc,mid+1,r,mid+1,R,d);
mx[x] = std::max(mx[lc],mx[rc]);
}
int n,m,c[MAXN],w[MAXN];
int lst[MAXN],pre[MAXN];
int main(){
read(n);read(m);
FOR(i,1,n) read(c[i]);
FOR(i,1,m) read(w[i]);
LL ans = 0;
FOR(i,1,n){
pre[i] = lst[c[i]];lst[c[i]] = i;
int p1 = pre[i],p2 = pre[p1];
modify(1,1,n,p1+1,i,w[c[i]]);
if(p1) modify(1,1,n,p2+1,p1,-w[c[i]]);
ans = std::max(ans,mx[1]);
}
printf("%lld\n",ans);
return 0;
}B
观察一下距离一个点直接距离为 $d$ 的图像是啥:
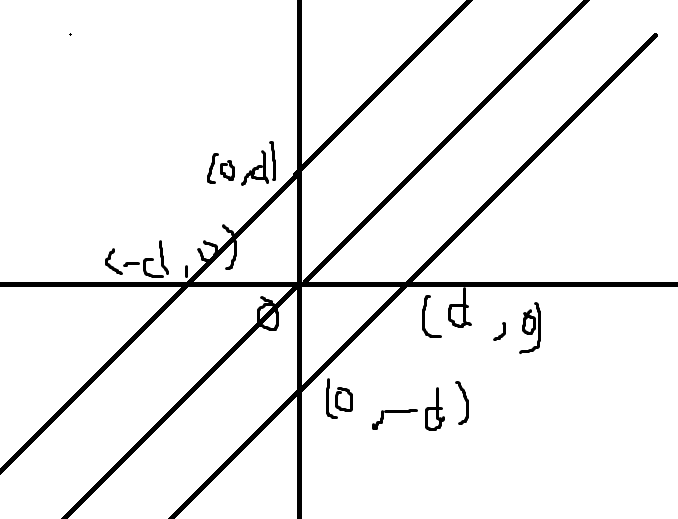
倾斜不是很好处理,于是我们旋转 $45$ 度,现在直接距离定义变成了 $\min(x_i-x_j,y_i-y_j)$。
然后我彩笔直接去扫描线,结果爆零了。。
我们先考虑如何求出距离最小值:发现这只可能会在相邻的 $x$ 坐标或者 $y$ 坐标产生。我们先将直接距离为 $0$ 的点都并起来,然后将点按照 $x$ 坐标排序,相邻的权值判断一下如果在不同连通块就能对答案产生贡献。
判断 $-1$ 只需要判断连通块大小是否是 $1$ 即可。
那么现在如何去计算方案数呢?一个 $O(n^2)$ 的想法是数连通块之间有多少条边,去重后每条边贡献是连通块大小乘积。我考试的时候自闭了。。
但是实际上发现这样的边只有 $O(n)$ 条:因为只会在按照某一维排序后相邻的点对中产生,所以去个重统计答案就行了。
发现就是没去写距离的式子。。被降智了。。
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 2e5 + 5;
int n;
struct Node{
int x,y,id;
Node(int x=0,int y=0,int id=0) : x(x),y(y),id(id) {}
}a[MAXN];
int f[MAXN],sz[MAXN];
inline int find(int x){
return x == f[x] ? x : f[x] = find(f[x]);
}
inline void merge(int x,int y){
x = find(x);y = find(y);
if(x == y) return;
f[x] = y;
}
std::map<P,int> S;
inline void addedge(int x,int y){
x = find(x);y = find(y);
if(x == y) return;
if(x > y) std::swap(x,y);
S[MP(x,y)] = 1;
}
int main(){
scanf("%d",&n);
FOR(i,1,n){
int x,y;scanf("%d%d",&x,&y);
a[i] = Node(x+y,x-y,i);f[i] = i;
}
std::sort(a+1,a+n+1,[&](const Node &x,const Node &y){return x.x < y.x;});
for(int l = 1,r;l <= n;l = r+1){
r = l;
while(r+1 <= n && a[r+1].x == a[r].x) ++r;
FOR(i,l+1,r) merge(a[i].id,a[i-1].id);
}
std::sort(a+1,a+n+1,[&](const Node &x,const Node &y){return x.y < y.y;});
for(int l = 1,r;l <= n;l = r+1){
r = l;
while(r+1 <= n && a[r+1].y == a[r].y) ++r;
FOR(i,l+1,r) merge(a[i].id,a[i-1].id);
}
std::sort(a+1,a+n+1,[&](const Node &x,const Node &y){return x.x < y.x;});
int ans = 1e9;
for(int l = 1,r;l <= n;l = r+1){
r = l;
while(r+1 <= n && a[r+1].x == a[r].x) ++r;
if(l-1 && find(a[l-1].id) != find(a[l].id)) ans = std::min(ans,a[l].x-a[l-1].x);
}
std::sort(a+1,a+n+1,[&](const Node &x,const Node &y){return x.y < y.y;});
for(int l = 1,r;l <= n;l = r+1){
r = l;
while(r+1 <= n && a[r+1].y == a[r].y) ++r;
if(l-1 && find(a[l-1].id) != find(a[l].id)) ans = std::min(ans,a[l].y-a[l-1].y);
}
if(ans == 1e9){
puts("-1");
return 0;
}
printf("%d\n",ans);
std::sort(a+1,a+n+1,[&](const Node &x,const Node &y){return x.x < y.x;});
for(int l = 1,r;l <= n;l = r+1){
r = l;
while(r+1 <= n && a[r+1].x == a[r].x) ++r;
if(l-1 && a[l].x-a[l-1].x == ans) addedge(a[l-1].id,a[l].id);
}
std::sort(a+1,a+n+1,[&](const Node &x,const Node &y){return x.y < y.y;});
for(int l = 1,r;l <= n;l = r+1){
r = l;
while(r+1 <= n && a[r+1].y == a[r].y) ++r;
if(l-1 && a[l].y-a[l-1].y == ans) addedge(a[l-1].id,a[l].id);
}
FOR(i,1,n) sz[find(i)]++;
LL res = 0;
for(auto x:S) res += 1ll*sz[x.fi.fi]*sz[x.fi.se];
printf("%lld\n",res);
return 0;
}C
可以发现这个操作本质是对 $1$ 的移动。移动问题可以考虑维护处什么时候移动了。
我们考虑对于每个 $1$,求出它在哪些时间往前移动了一格,我们用一个 $01$ 串表示,第 $i$ 位是 $1$ 表示在时间 $i$ 这个 $1$ 往前移动了一格。如果能对于每个 $1$ 都求出来这个,就能求出每个 $1$ 最后到了哪里。
我们一开始是一个全 $0$ 的串,考虑有了第 $i$ 个 $1$ 的串,如何转移到第 $i+1$ 个 $1$ 的串?如果下一个 $1$ 和这个 $1$ 是相邻的,可以发现如果在第 $i$ 个位置的第 $j$ 个时刻往前移动了一次,那么第 $i+1$ 的第 $j+1$ 个时刻也会往前移动,所以相当于是做一个右移操作,删除最后一个数字,并且在最前面加上一个 $0$。
如果和下一个 $1$ 中间有 $c$ 个 $0$,那么相当于还可以将这个序列的前 $c$ 个 $0$ 变成 $1$,相当于可以抵消 $c$ 次上一个不动但是这一个动的情况。
所以我们要支持如下操作:循环右移一位,将前 $c$ 个 $0$ 变成 $1$。于是我们考虑直接维护 $0$ 在序列中的位置,相当于要支持从后端删除,从前端插入,从前端删除,全局加,用双端队列+全局 tag 就可以解决了。
如何算逆序对呢?我们考虑每次加入一个 $1$ ,它对哪些轮有贡献:显然这个 $1$ 会一直右移,移动到最后面出去就结束了,在它经过的所有时间答案都会 $+1$,根据这个在序列中的位置可以算出多少时间后它会被弹掉,就能确定他贡献的一段区间,差分即可。
这种题就是我完全想不到吧。。如果发现本质是对谁的移动就可以考虑什么时候移动
#include <bits/stdc++.h>
#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int ha = 998244353;
const int MAXN = 5e6 + 5;
LL ans;
int b=1;
inline void add(int &x,int y){
x += y-ha;x += x>>31&ha;
}
inline void answer(int val){
ans ^= (1ll*val*b%ha);
b = 233ll*b%ha;
}
char str[MAXN];
int n,T;
std::vector<int> ps;
bool vis[MAXN];
int cf[MAXN];
int main(){
scanf("%d",&T);scanf("%s",str+1);n = strlen(str+1);
FOR(i,1,n) if(str[i] == '1') ps.pb(i);
std::deque<int> q;int tag = 0;int las = 0;
FOR(i,1,T) q.pb(T-i);int rem = (int)ps.size();
for(auto x:ps){
int cur = x-las-1;--rem;
if(!q.empty() && q.back()+tag == 0) q.pop_back();
tag--;
q.push_front(T-1-tag);
while(!q.empty() && cur--){
int pos = T-(q.front()+tag);
cf[pos]++;cf[pos+rem+1]--;
q.pop_front();
}
vis[x-(T-(int)q.size())] = 1;
// if(x == 4){
// for(auto y:q) DEBUG(y+tag);
// }
las = x;
}
FOR(i,1,n) putchar(vis[i]+'0');puts("");
FOR(i,1,T) add(cf[i],cf[i-1]);
int sm = 0;
ROF(i,n,1){
if(str[i] == '0') sm++;
else add(cf[0],sm);
}
FOR(i,1,T) add(cf[i],cf[i-1]);
FOR(i,0,T) answer(cf[i]);
printf("%lld\n",ans);
return 0;
}