A
暴力枚举每个字母对应的括号即可。$O(2^3 n)$
B
发现行列之间的影响只会在于四个角上,所以暴力枚举四个角是否填,然后确定上下界判断即可。$O(2^4)$。
C
显然 $a_i,b_i > 0$ 和 $a_i,b_i < 0$ 可以分开做:我们只考虑 $a_i,b_i > 0$ 的情况。
排序之后,我们枚举「推」到的最后一个位置是 $b_x$,那么我们找到 $\leq b_x$ 的 $a$ 数量,设为 $y$,我们相当于就是占据了 $[b_x-y+1,b_x]$ 的所有格子,和 $(b_x,\infty)$ 的所有已经在目标位置上的格子。前者直接二分就可以找到 $y$ 和那个区间里有几个目标格子,后者处理一个后缀和表示 $ \geq b_i$ 的位置有几个是不用动就放好的就行了。$O(n \log n)$
D
由于要求每个人至少有两个下属,并且要求值是严格下降的,所以我们考虑从高到低去递归构造。
由于题目保证有解,设我们现在正在构造 $S$ 内的点构成的树。如果不是要求父亲严格比儿子大,我们随便找出一对 $u,v \in S$,满足 $a_{u,v}$ 是当前能取到的最大值,将剩下的点 $x$ 分为三类:
- $a_{u,x}<mx,a_{v,x}=mx$
- $a_{u,x} = a_{v,x} = mx$
- $a_{u,x}=mx,a_{v,x}<mx$
新建一个点 $r$,令 $val_r = a_{u,v}$,那么一类点一定要放在左儿子,三类点一定要放在右儿子,二类点随便安排就好了。
但是要注意:如果二类点的个数 $\geq 3$,按照上面的构造方法我们会在下面也加入一个 $val_r$,所以这样不满足严格了。
我们对于两个点 $(u,v)$,如果 $a_{u,v}=mx$,就连边 $u,v$。然后我们随便找出一个极大团,剩下的点 $x$ 一定和极大团中至少一个点 $y$ 满足 $a_{x,y}<mx$。那么就把它分配到 $y$ 对应的子树内就好了。同理,我们不可能出现和 $\geq 2$ 个最大团里的点 $y$ 满足 $a_{x,y}<mx$ 的情况。时间复杂度为 $O(n^3)$。可能可以优化。
E
遇到判定回文串的问题,我们可以考虑按照长度进行奇偶分类,然后不断去每次删掉开头结尾,去寻找剩下的最短串是否可以构造出来。
将 $k$ 分类讨论:
$k$ 是奇数
如果存在一个长度为 $k$ 的路径,那么每次我们可以删去开头和结尾,仍然是满足条件的。最后可以得到一个长度为 $3$ 的路径,大概是

也就是,只要有一对点之间有双向边,就一定能构造出 $k \geq 3$,$k$ 是奇数的所有路径。可以发现这个条件和存在一条长度为 $k$ 的路径是等价的。(因为两个方向上面我们都推过了)
$k$ 是偶数
类似上面的思想,我们最后会缩成以下情况:
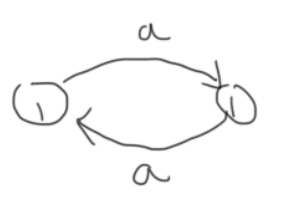
也就是说只要有一对点之间有双向边并且字母相同,我们就可以构造出 $k \geq 2$,$k$ 是偶数的所有路径。也是等价的。
具体维护的时候,更改某条边就看看有没有反方向的边,算算影响就好了~
F
不难发现如果奇点数量 $\leq 2$ 的话直接找出一个欧拉路径就做完了。
我们考虑什么时候我们应该切换模式,也就是考虑切换模式后的状态能清空哪些图:
首先有环肯定不行(这里指的长度 $\geq 3$ 的环),因为环走一遍之后会消去一半的边,就继续走不下去了。
一条 $\geq 4$ 长度的链也不行,这个手动模拟一下也能看出来。
所以我们只能做:直径 $\leq 3$ 的树,发现这好像就是菊花图!!1
于是我们考虑先找出一个路径,使得剩下没被经过的边恰好构成一个菊花图,并且中心是这个路径的终点。
赛时有一个 naive 的想法:直接令中心为连接所有奇点的点,然后去做。发现 WA on test 19 然后比赛结束了。。。
赛后想到了一种特殊情况是,删掉这个菊花图后还有两个奇点,所以我找的中心改成连接奇点的数量 $\leq odd-2$,如果只有 $odd-2$ 个考虑找一条欧拉路径并且终点是中心。然后 WA on test 38。。。。并且比赛的时候只会测前 $37$ 个点,所以一堆人 fst 了。
test 38 是一个很小的数据,大概长这样:
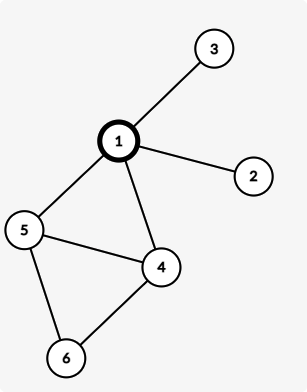
我们就会选择 $1$ 点作为中心,然后把边 $1 \to (2,3,4,5)$ 全都删了,就无法到达 $1$ 了。会判断为无解。
这种问题只会和菊花图的某一个叶子有关,也就是说这个图不能长这样,否则无解(不会证,):
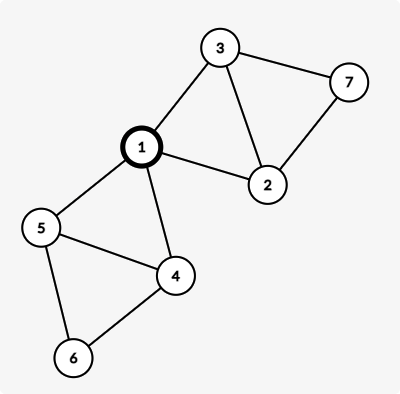
那么我们就枚举中心,找到所有叶子。先看看有没有直接到达中心的欧拉路径,如果没有的话,枚举某个叶子不删除然后接着找就行了。复杂度 $O(nm)$ 。由于现在 open hacking 还没有结束,随时可能被 hack。
