题意
有一条长度为 $n+1$ 的村庄,编号依次为 $0\ldots n$。最初,在 $i$ 和 $i+1$ 之间有双向通行的铁路。
现在有两个铁路公司(A 和 B)要争夺这些村庄。$0$ 和 $n$ 这两个村庄同时被两个铁路公司占有,$[1,n-1]$ 内的村庄会被其中一个铁路公司占有。
假设某个铁路公司占有的村庄按顺序排序为 $a_1,a_2,\ldots,a_m$,那么在 $(a_1,a_2),(a_2,a_3),\ldots,(a_{m-1},a_m)$ 之间也会有一条双向铁路。
现在已经确定了某些村庄的分配情况,需要求出有多少种分配剩下的村庄的方案,使得从 $0$ 到 $n$ 的最短路 $\leq k$ 。每条铁路经过的时间都为 $1$。对 $10^9+7$ 取模。
$n \leq 4000$
题解
神仙题。。。
启发:很多转移带环的最短路问题,如果最后有要求按照某个顺序 dp 的话,可以考虑这个环会影响哪些情况,有时候可以「假设」满足这些情况,然后发现在假设不成立的时候这个限制是更松的,就可以对了。
还是按照套路,先考虑如何判定某个状态是否合法:我们就从 $0$ 开始按照边跑一个 bfs,判断一下 $n$ 位置的最短路是否 $\leq k$ 就好了。
所以如果想计数的话,应该是把这个最短路过程压入 dp 状态。直接暴力记录所有点的 $dis_v$ 数组显然不可以,所以我们考虑一下这个图的最短路有没有什么特别之处。
这个题由于是无向边,最短路需要考虑如何处理往回走的情况。发现往回走到达某个点是最短路,当且仅当它在一大块和它一样的字母中,这样先跳到后面的那个字母,再倒着走回来。
也就是说,倒着走是这种情况:
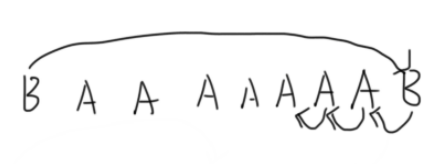
这样会比正着走可能要快一点。其实就是相当于花费了 $2$ 的代价,可以倒着遍历。
也就是说,我们每次扩展一个新的字符,如果这个字符的最短路最后一步是从右边过来的,那么一定是从它右边的第一个和它不一样的位置过来的(中间可能经过多个一样的位置)。
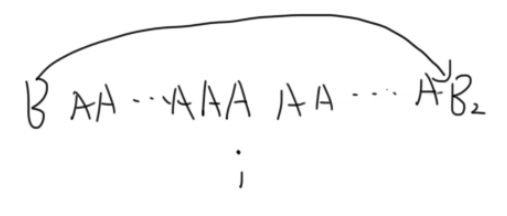
还是以 $i$ 位置的 A 举例,首先如果倒着走,一定是有一次从 $i$ 的前面跑到 $i$ 的后面了,而 A 显然不可能跨过中间的 A 直接到后面的 A,所以只有可能是从 $i$ 前面的 B 跳到了后面,然后后面这个 B 到 $i$ 这一段一定全是 A(因为恰好是下一个 B),所以只能一步步倒回去。所以也不会多次跨过 A(因为无论如何都在 A 后面第一个 B 停下)。
联想到在结束的时候最后一个位置一定同时是 A 和 B,所以我们在考虑一段的时候可以假设这一段后面就是和它不一样的一个字母(也就是支持倒着走)。
设 $f_{i,j,k,0/1}$ 表示考虑了前 $i$ 个位置,当前位置的最短路是 $j$,和当前位置不同的字母最靠后的位置的最短路是 $k$,当前位置的字母是 A/B,假设下一个字母和当前位置的字母不同的方案数。
转移我们以要填 A 为例。
如果 $i+1$ 位置是 A,$i$ 位置是 B:那么还是维持之前的假设的,所以 $j,k$ 这两个最短路可以直接拿过来用,转移就考虑从 B 走过来($k+1$)还是从上一个 A 走过来($j+1$)就好了。
如果 $i+1$ 位置是 A,$i$ 位置也是 A:这时候就破坏了之前的假设,考虑是否能 fix。如果想从上一个 B 转移过来,看起来是不影响的,因为我们接下来要假设 $i+1$ 后面一个位置是不同的,所以用 $k+2$ 更新;如果想从上一个 A 转移过来,要讨论一下:
- 如果上一个 $A$ 的最短路没有通过假设的 $B$ 走过来的,说明这个最短路还是对的,用 $j+1$ 更新;
- 如果上一个 $A$ 的最短路是倒着从假想的 $B$ 走过来的,如果我们用 $j+1$ 更新,肯定会比 $k+2$ 大(因为这实际上是用 $k+3$ 更新:上一次这个 $j$ 是用 $k+2$ 更新,这次又要 $+1$),所以这个问题不用担心
对于填 B 是类似的。复杂度 $O(n^3)$。
优化的话,考虑在这个假设下,$|j-k| \leq 2$(因为可以花最多 $2$ 步相互到达),所以就可以优化到 $O(n^2)$ 了。
代码
#include <bits/stdc++.h>
#define fi first
#define se second
#define DB double
#define U unsigned
#define P std::pair
#define LL long long
#define LD long double
#define pb emplace_back
#define MP std::make_pair
#define SZ(x) ((int)x.size())
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 4000 + 5;
const int ha = 1e9 + 7;
const int off = 2;
int n,k;
char str[MAXN];
int f[2][MAXN][5][2],now;
// [-2,2]
inline void add(int &x,int y){
x += y-ha;x += x>>31&ha;
}
int main(){
scanf("%d%d",&n,&k);
scanf("%s",str+1);
CLR(f[now=0],0);
if(str[1] != 'B') f[now][1][-1+off][0] = 1;
if(str[1] != 'A') f[now][0][1+off][1] = 1;
FOR(i,2,n-1){
CLR(f[now^1],0);
FOR(j,0,n){
FOR(k,-2,2){
int c0 = f[now][j][k+off][0],c1 = f[now][j][k+off][1];
if(!c0 && !c1) continue;
int d0 = j,d1 = j+k;
if(str[i] != 'B'){
int dis = std::min(d0+1,d1+2);
add(f[now^1][dis][d1-dis+off][0],c0);
dis = std::min(d0+1,d1+1);
add(f[now^1][dis][d1-dis+off][0],c1);
}
if(str[i] != 'A'){
int dis = std::min(d0+1,d1+1);
add(f[now^1][d0][dis-d0+off][1],c0);
dis = std::min(d0+2,d1+1);
add(f[now^1][d0][dis-d0+off][1],c1);
}
}
}
now ^= 1;
}
int ans = 0;
FOR(i,0,n){
FOR(j,-2,2){
int da = i,db = i+j;
if(da >= k && db >= k) continue;
FOR(k,0,1){
add(ans,f[now][i][j+off][k]);
}
}
}
printf("%d\n",ans);
return 0;
}

One comment
讲得太好了终于看懂了 qwq!