<h1>定义</h1>

什么叫平衡树？就是看起来很平衡的树。

它是一种中序遍历有序的一棵搜索树，满足左儿子的权值<自身权值<右儿子的权值

它是递归定义的。

<h1>算法</h1>

目前平衡树的算法很多，在OI中，我们常使用Treap和Splay<(set)

平衡的概念有高度平衡，重量平衡等。

高度平衡是指对于一个大小为N的树，深度不超过 $log_{ \frac{1}{\alpha} } (N + 1)​$

大小平衡是指对于一个数，满足：$ max (left,weight,right.weight)\leq \alpha \cdot weight $

对于高度平衡，所有平衡树算法几乎都满足，而Treap 替罪羊树还能同时满足重量平衡。

那么怎么调节平衡呢？我们通过旋转来调节。请看下图

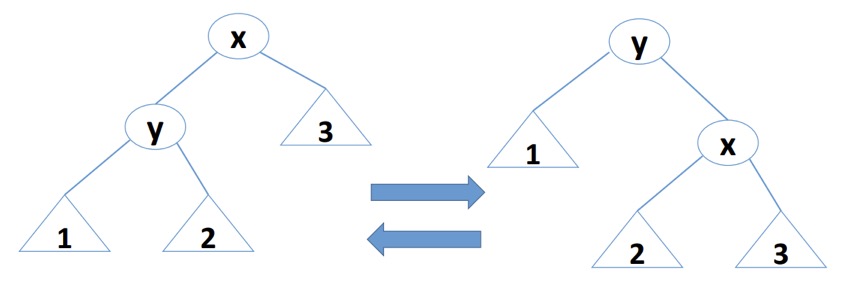
其实究竟是左旋还是右旋不必搞那么清楚，可以按照自己的理解来，我的理解就是将左边的结点向右提就是右旋。

<h3>Treap</h3>

Treap 是一个平衡树

它在维护数据 key 的同时，维护了一个额外数据 weight

weight 是纯随机的数据，保证 key 满足平衡树的同时，weight满足一个堆.如下图就是一个Treap的形式：

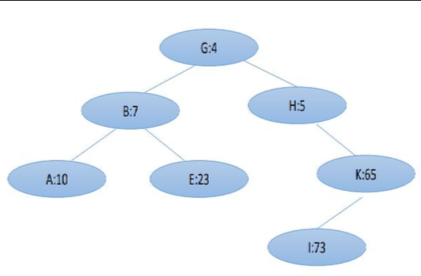
Treap支持在 $log_2N$ 的时间复杂度内完成插入，删除，查询等操作。

<h4>插入</h4>

我们先按照二叉树的方式插入，如果Treap的性质被破坏，那么就通过旋转来维护Treap的性质。以下为插入图解:

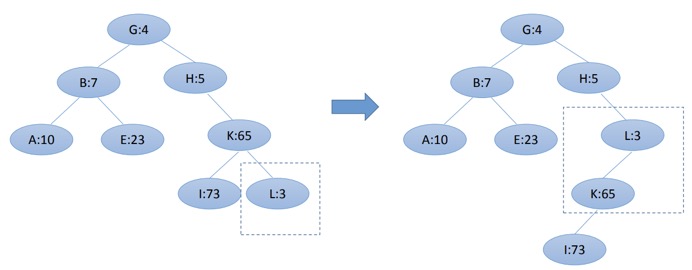
先直接添加，然后发现违反了Treap的性质，所以旋转

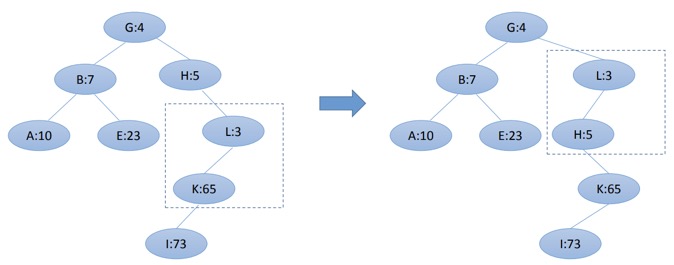
一直旋转，直至旋转到根。

这样插入操作就结束了。

<h4>删除</h4>

因为删去一个叶子节点完全不破坏 Treap 的性质，不断尝试将根节点旋转
到叶子节点，然后删之即可(也可以认为根节点的权值变为+∞)

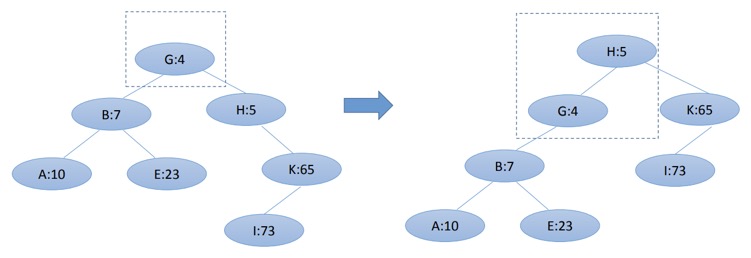
开始向下旋转

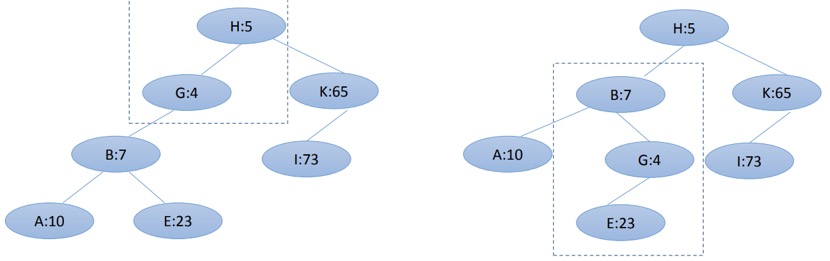
继续旋转，保持Treap性质

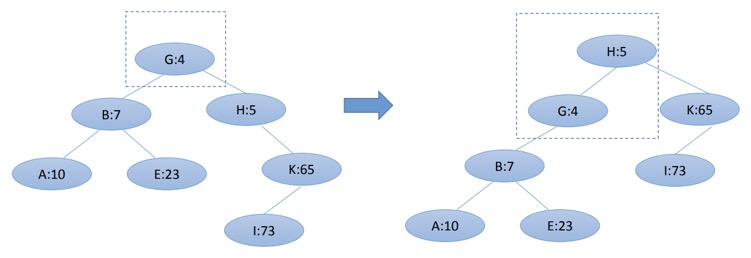
旋转

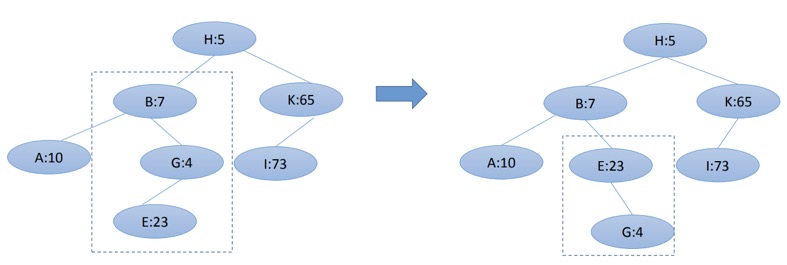
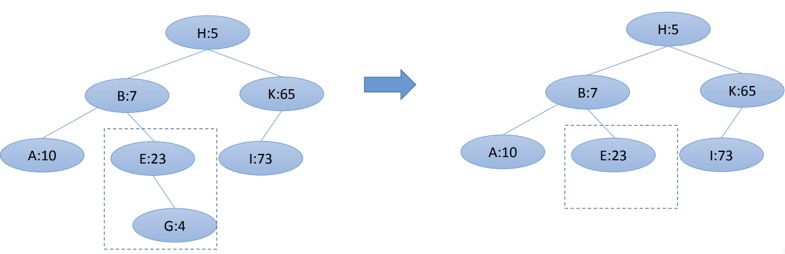
移除，这样删除操作就完成了。

<h3>代码实现</h3>

以普通平衡树为例

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <ctime>

int ans,N,x,y;

struct Node{
    int key,priority; //key表示键值，priority表示优先级
    int size,num; //size表示该树的结点数量，num表示当前结点元素的数量（相同的元素数量）
    Node *ch[2]; //左右子树指针

    Node(){
        key = 0;
        priority = rand();
        size = num = 1;
        ch[0] = ch[1] = NULL;
    }
    void push(){ //更新
        size = num;
        if(ch[0] != NULL)
            size += ch[0]->size;
        if(ch[1] != NULL)
            size += ch[1]->size;
    }
}*root;

void rotate(Node *&v,int d){
    Node *t = v->ch[d^1];
    v->ch[d^1] = t->ch[d]; //改变t的子树位置
    t->ch[d] = v; //将t旋转到v上方
    v->push(); //先更新v再更新t
    t->push();
    v = t; //将t旋到v
}

void insert(Node *&v,int x){
    if(v == NULL){ //没有点就新建一个点
        v = new Node;
        v->key = x;
        return;
    }
    if(v->key == x){ //重复元素直接累加
        v->size++;
        v->num++;
        return;
    }
    if(x < v->key){ //x较小，插入左子树
        insert(v->ch[0],x);
        if(v->ch[0]->priority < v->priority) //旋转维护treap的重量平衡
            rotate(v,1);
        else v->size++; //直接更新
    }
    else{ //x较小，插入右子树
        insert(v->ch[1],x);
        if(v->ch[1]->priority < v->priority)
            rotate(v,0);
        else v->size++;
    }
}

void remove(Node *&v,int x){
    if(v == NULL) //不合法退出
        return;
    if(x == v->key){ //相等则删除
        if(v->num > 1){ //有多个相等元素，减少数量即可
            v->size--;
            v->num--;
            return;
        }
        else{ //需要完全删除
            if(v->ch[0] == NULL){ //左子树为空，将右子树移到结点上
                Node *t = v;
                v = v->ch[1];
                free(t);
                return;
            }
            if(v->ch[1] == NULL){ //右子树为空，将左子树移到结点上
                Node *t = v;
                v = v->ch[0];
                free(t);
                return;
            }
            //左右子树非空，将该结点向下旋转。
            if(v->ch[0]->priority < v->ch[1]->priority){ //左子树优先级小，为了维护treap的性质，将左子树向上旋转，作为当前树新的根结点
                rotate(v,1);
                remove(v->ch[1],x);
            }
            else{ //右子树优先级小，为了维护treap的性质，将右子树向上旋转，作为当前树新的根结点
                rotate(v,0);
                remove(v->ch[0],x);
            }
            v->size--; //删除后，更新根结点信息
        }
    }
    else{ //这个结点不需要删除
        if(x < v->key) //目标删除更小，去左子树删除
            remove(v->ch[0],x);
        else //目标删除更大，去右子树删除
            remove(v->ch[1],x);
        v->size--;
    }
}

int getk(Node *v,int x){ //询问x数的排名
    int s = 0; //s记录左子树的结点数量
    if(v->ch[0] != NULL) //判定这个结点的有无
        s = v->ch[0]->size;
    if(x <= s) //节点位于左子树内，排名为左子树内的排名
        return getk(v->ch[0],x);
    if(x <= s + v->num) //当前结点就是求的结点
        return v->key;
    else
        return getk(v->ch[1],x - s - v->num);  //节点位于左子树内，排名为左子树的元素数量 + 当前树根的结点元素数量 + 其在右子树中的排名
}

int getrank(Node *v,int x){ //查询排名是x的数
    int s = 0;  //s记录左子树的结点数量
    if(v->ch[0] != NULL) //判定这个结点的有无
        s = v->ch[0]->size;
    if(x < v->key)
        return getrank(v->ch[0],x); //目标结点位于左子树内，则其当前的排名是在左子树的排名
    if(x == v->key)
        return s + 1; //目标结点就是本结点
    else
        return s + v->num + getrank(v->ch[1],x); //目标结点位于右子树内，则其当前的排名是在右子树的排名
}

void pre(Node *v,int x){ //寻找x的前驱
    if(v == NULL) //不合法退出
        return;
    if(v->key < x){ //当前键值为可行解
        ans = v->key; //保存可行解
        pre(v->ch[1],x); //寻找更优解
    }
    else
        pre(v->ch[0],x); //不是可行解，返回
}

void succ(Node *v,int x){ //寻找x的后继
    if(v == NULL) return; //不合法退出
    if(v->key > x){ //当前键值为可行解
        ans = v->key; //保存可行解
        succ(v->ch[0],x); //寻找更优解
    }
    else
        succ(v->ch[1],x); //不是可行解，返回
}

int main(){
    srand(time(0));
    scanf("%d",&N);
    while(N--){
        scanf("%d%d",&x,&y);
        switch(x){
            case 1:
                insert(root,y);
                break;
            case 2:
                remove(root,y);
                break;
            case 3:
                printf("%dn",getrank(root,y));
                break;
            case 4:
                printf("%dn",getk(root,y));
                break;
            case 5:
                pre(root,y);
                printf("%dn",ans);
                break;
            case 6:
                succ(root,y);
                printf("%dn",ans);
                break;
        }
    }
    return 0;
}

<h2>Splay</h2>

Splay 维护平衡不需要额外的数据,其基本思路是数据访问的”二八规则“—— 80% 的人只用到 20% 的数据，所以有些常用的数据应当位于比较浅的位置
所以每次访问到一个节点的时候，都把该节点直接旋转到根
核心操作:splay(x) (把 x 节点旋转成根)

时间复杂度:均摊 $$\Theta(log_2N)$$

<h3>误区</h3>

不要使用Treap的旋转方式来对Splay进行旋转，这不叫Splay，这叫Spaly，时间复杂度为$$\Theta(玄学)$$

我们把 Treap 的旋转称为单旋，接下来我们要学的另一种适用于Splay的旋转：双旋

<h3>旋转</h3>

有两种旋转方式。

一字型旋转适用于在同一子树时的情况，具体如图：

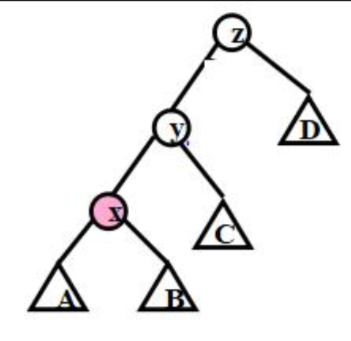旋转为

​

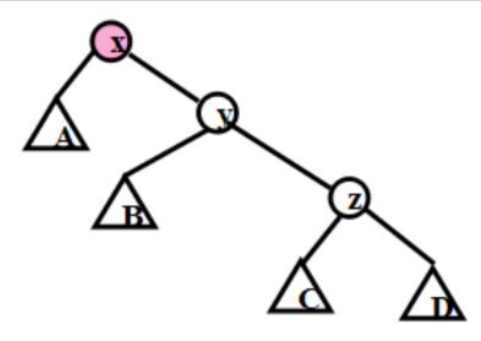
​ 工字型旋转适用于两个结点不在同一子树里的时候，具体看图：

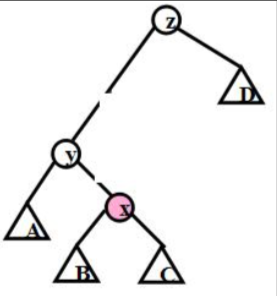旋转为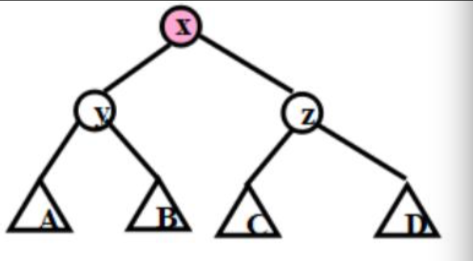

<h3>过程</h3>

把 X 反复双旋，直到 X 为根或者根的儿子
如果 X 是根的儿子，则 X 单旋

如果 X 是根，过程结束

<h3>代码实现</h3>

以普通平衡树为例

#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>

namespace splay{
    const int inf = 0x7fffffff;
    struct Node *nil;
    struct Node{
        Node *ch[2];
        int val,cnt,size; //val表示元素的值，cnt表示个数，该结点的子树包含元素的个数
        int cmp(int v){  //返回寻找v应该向左走还是向右走
            if(v == val) return -1;
            return v < val ? 0 : 1;
        }
        int cmpk(int k){ //同上，只不过是寻找第k小
            if(k <= ch[0]->size)
                return 0;
            if(k <= ch[0]->size + cnt)
                return -1;
            return 1;
        }
        void push(){
            size = cnt + ch[0]->size + ch[1]->size;
        }
        Node(int v) : val(v),cnt(1),size(1) {ch[0] = ch[1] = nil;}
    } *root;

    void init(){
        nil = new Node(0);
        root = nil->ch[0] = nil->ch[1] = nil;
        nil->size = nil->cnt = 0;
    }

    void rotate(Node *&t,int d){
        Node *k = t->ch[d ^ 1];
        t->ch[d ^ 1] = k->ch[d];
        k->ch[d] = t;
        t->push();k->push();
        t = k;
    }

    void splay(int v,Node *&t){ //在树t中寻找值为v的节点，并伸展成为t的根节点
        int d = t->cmp(v); // 定义方向
        if(d != -1 && t->ch[d] != nil){
            int d2 = t->ch[d]->cmp(v);
            if(d2 != -1 && t->ch[d]->ch[d2] != nil){
                splay(v,t->ch[d]->ch[d2]);
                if(d == d2)
                    rotate(t,d2^1),rotate(t,d^1);
                else
                    rotate(t->ch[d],d2^1),rotate(t,d ^ 1);
        }
        else rotate(t,d ^ 1);
    }
}

void splayk(int k,Node *&t){  //在树t中寻找第K小的节点，并伸展成为t的根节点
    int d = t->cmpk(k);
    if(d == 1)
        k -= t->ch[0]->size + t->cnt;
    if(d != -1){
        int d2 = t->ch[d]->cmpk(k);
        int k2 = (d2 == 1) ? k-(t->ch[d]->ch[0]->size + t->ch[d]->cnt) : k;
        if(d2 != -1){
            splayk(k2,t->ch[d]->ch[d2]);
            if(d == d2)
                rotate(t,d2^1),rotate(t,d^1);
            else
                rotate(t->ch[d],d2^1),rotate(t,d^1);
        }
        else rotate(t,d^1);
    }
}

int pre(int v,Node *&t = root){ //前驱,找左边
    splay(v,t);
    if(t->val >= v){
        if(t->ch[0] == nil)
            return -inf;
        splay(inf,t->ch[0]);
        return t->ch[0]->val;
    }
    else
        return t->val;
}

int succ(int v,Node *&t = root){ //后继，找右边
    splay(v,t);
    if(t->val <= v){
        if(t->ch[1] == nil)
            return inf;
        splay(-inf,t->ch[1]);
        return t->ch[1]->val;
    }
    else
        return t->val;
}

int getrank(int v,Node *&t = root){ //求排名为v的结点
    splay(v,t);
    return t->ch[0]->size + 1;
}

int getk(int k,Node *&t = root){ //求第K大
    splayk(k,t);
    return t->val;
}

Node split(int v,Node &t){ //分裂,树t都是小于等于X的元素，返回的树都是大于X的元素
    if(t == nil)
        return nil;
    splay(v,t);
    Node t1,t2;
    if(t->val <= v){
        t1 = t;t2 = t->ch[1];t->ch[1] = nil;
    }
    else{
        t1 = t->ch[0];t2 = t;t->ch[0] = nil;
    }
    t->push();
    t = t1;
    return t2;
}

void merge(Node &t1,Node &t2){
    if(t1 == nil)
        std::swap(t1,t2);
    splay(inf,t1);
    t1->ch[1] = t2;
    t2 = nil;
    t1->push();
}

void insert(int v,Node *&t = root){
    Node *t2 = split(v,t);
    if(t->val == v)
        t->cnt++;
    else{
        Node *node = new Node(v);
        merge(t,node);
    }
    merge(t,t2);
}

void erase(int v,Node *&t = root){
    Node *t2 = split(v,t);
    if(t->val == v && --(t->cnt) < 1){
        Node *t3 = t->ch[0];
        delete t;
        t = t3;
    }
    merge(t,t2);
}
}

int main(){
    splay::init();
    int N,opt,x;
    scanf("%d",&N);
    while(N--){
        scanf("%d%d",&opt,&x);
        switch(opt){
            case 1:
                splay::insert(x);
                break;
            case 2:
                splay::erase(x);
                break;
            case 3:
                printf("%dn",splay::getrank(x));
                break;
            case 4:
                printf("%dn",splay::getk(x));
                break;
            case 5:
                printf("%dn",splay::pre(x));
                break;
            case 6:
                printf("%dn",splay::succ(x));
                break;
        }
    }
    getchar();getchar();
    return 0;
}

<h1>最后</h1>

掌握了模板才是学习的开始，尝试去独立切一些平衡树题目吧！Good Luck！