<h1>定义</h1>
对一个简单多边形来说,如果给定其边界上或内部的任意两个点,连接这两个点的线段上的所有点都被包含在该多边形的边界上或内部的话,则该多边形为凸多边形 。
一般有两种方法:Graham 扫描法和 Jarvis 步进法。但是由于作者本人姿势水平有限,这里只介绍 Graham 扫描法。
<h1>前置芝士</h1>
为了写成一篇让像我这种的初中生能读懂的文章,我先写一些需要先了解到的东西。
<h2>计算集合中的相等</h2>
由于计算机处理浮点数的特殊性,我们可以设置一个常量 $EPS$ ,规定两个数相等为他们的差的绝对值小于等于 $EPS$ 。
const double EPS = 1e-9; // or smaller than
inline bool equ(double x,double y){
return std::fabs(x-y) < EPS;
}
<h2>向量</h2>
<h3>定义</h3>
向量是有大小有方向的量。在几何中,它被表示为带箭头的线段。向量可以用起点和终点的坐标来表示。
$\vec{AB}$ 同时也可以使用 $(^{x_A−x_B}_{y_A−y_B})$ 来表示。
struct Point{ // 为了方便使用点和向量混合定义的方式
double x,y;
Point() {}
Point(double x,double y) : x(x),y(y) {}
}
<h3>向量的模</h3>
就是这个向量的长度。对于 $a=(^x_y)$ ,它的长度 $|a|=\sqrt{x^2+y^2}$ 。
double len(){
return std::sqrt(xx+yy);
}
<h3>向量的运算</h3>
注意到点和点的差是一个向量,点和向量的和或差是一个点。
本篇文章只会用到点和点的差,故只给出此代码。
Point operator - (const Point &t) const {
return Point(x-t.x,y-t.y);
}
<h3>向量的点积</h3>
$a \cdot b$ 的几何意义是 $a$ 在 $b$ 上的投影长度乘上 $b$ 的模长。
$ a\cdot b=|a||b| \cos \theta $ ,其中 $\theta$ 是一个区分正负的夹角。
$$ a⋅b=x_1y_1+x_2y_2 $$
<h4>基本运用</h4>
判断两个向量是否垂直:$ a⊥b⇔a⋅b=0$
求两个向量的夹角:若$ a⋅b>0$ 则夹角为锐角,若 $a⋅b<0$ ,则夹角为钝角。
<h3>二维叉积</h3>
两个向量的叉积是一个标量,$a \times b$ 的几何意义为他们所形成的平行四边形的有向面积。
double operator * (const Point &t) const {
return xt.y - yt.x;
}
<h4>基本应用</h4>
可以判断 $b$ 在 $a$ 的什么方向,如果叉积 $a\times b$ 结果 $>0$ 则顺时针,反之则逆时针。
还可以计算有向多边形的面积,依次将每个边叉一下就可以了。
<h2>极坐标系</h2>
<h3>定义</h3>
极坐标系是指在平面内由极点、极轴和极径组成的坐标系。在平面上取定一点$O$ ,称为极点。从 $O$ 出发引一条射线 $Ox$ ,称为极轴。再取定一个单位长度,通常规定角度取逆时针方向为正。这样,平面上任一点 $P$ 的位置就可以用线段 $OP$ 的长度 $ρ$ 以及从 $Ox$ 到 $OP$ 的角度 $θ$ 来确定,有序数对 $(ρ,θ)$ 就称为 $P$ 点的极坐标,记为 $P(ρ,θ)$ ;$ρ$ 称为 $P$ 点的极径,$θ$ 称为 $P$ 点的极角。
<h3>极角排序</h3>
这里我们介绍利用叉积的排序。
如果在同一直线上(叉积为 $0$ )那么我们可以比较距离极点的距离,否则就用两个向量 $ a=\vec{OA},b=\vec{OB}$ 叉一下来判断谁距离极轴的距离近(顺时针)距离远(逆时针)就可以了。
以 $p_1$ 为极点的 compare 自定义函数如下:
bool cmp(const Point &a,const Point &b){
return std::fabs((a-p[1])(b-p[1])) < EPS ? (a-p[1]).len() < (b-p[1]).len() : (a-p[1])(b-p[1]) > 0;
}
现在已经学完了基础知识了QAQ。
<h1>Graham扫描法</h1>
基本思想:通过设置一个关于候选点的堆栈 $S$ 来解决凸包问题。
操作:输入集合 $Q$ 中的每一个点都被压入栈一次,非 $CH(Q)$ (表示 $Q$ 的凸包)中的顶点的点最终将被弹出堆栈,当算法终止时,堆栈 $S$ 中仅包含 $CH(Q)$ 中的顶点,其顺序为个各顶点在边界上出现的逆时针方向排列的顺序。
大致过程是首先选择一个纵坐标最小的点作为极点,以正右为正方向建立极坐标系。将其他的点按照极角进行排序。每次遇到一个新的点时,不断弹出向内拐的点直到栈顶的点和新的点组成的向量是向外拐的,然后加入栈,遍历下一个点。
我们来看一个具体的例子: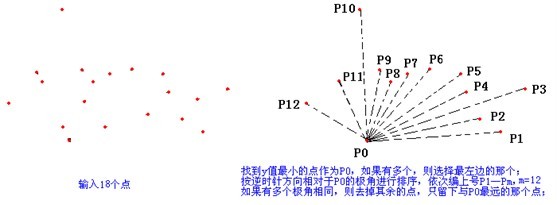
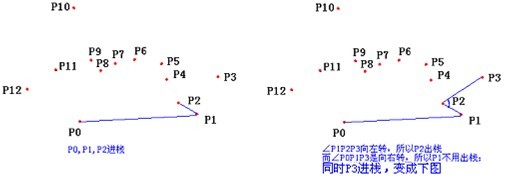
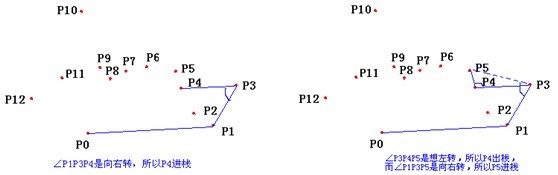
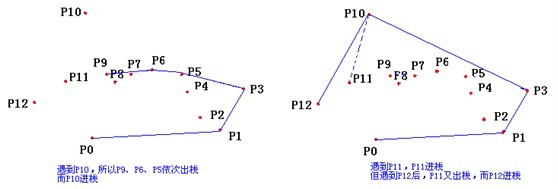
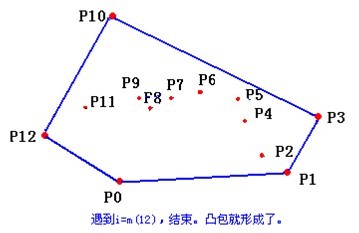
如果你想求出凸包面积,只需要按照顺时针叉一遍加起来就可以了。
具体代码如下:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 200000+5;
const double EPS = 1e-9;
inline bool equ(double x,double y){
return std::fabs(x-y) < EPS;
}
struct Point{
double x,y;
Point() {}
Point(double x,double y) : x(x),y(y) {}
Point operator - (const Point &t) const { // 点减法
return Point(x-t.x,y-t.y);
}
double operator * (const Point &t) const { // 叉积
return xt.y - yt.x;
}
bool operator < (const Point &t) const { // 找出极点
return equ(x,t.x) ? y < t.y : x < t.x;
}
bool operator == (const Point &t) const { // 判断同一个点
return equ(x,t.x) && equ(y,t.y);
}
double len(){ // 模长
return std::sqrt(xx+yy);
}
}p[MAXN],S[MAXN];
int top;
bool cmp(const Point &a,const Point &b){
return std::fabs((a-p[1])(b-p[1])) < EPS ? (a-p[1]).len() < (b-p[1]).len() : (a-p[1])(b-p[1]) > 0;
// 同一直线比较长度否则比较谁在右侧
}
int N;
int main(){
scanf("%d",&N);
FOR(i,1,N) scanf("%d%d",&p[i].x,&p[i].y);
std::sort(p+1,p+N+1); // 最小的 p
std::sort(p+2,p+N+1,cmp); // 极角排序
N = std::unique(p+1,p+N+1)-(p+1);
FOR(i,1,N){
while(top > 1 && (p[i]-S[top-1])*(S[top-1]-S[top-2]) > 0) // 这个点在逆时针方向弹掉
top--;
S[top++] = p[i];
}
double ans = 0.0;
FOR(i,0,top-1){
ans += S[i]*S[(i+1)%top];
}
printf("%.5f",ans);
return 0;
}
执行完代码后,$S$ 中就是凸包按逆时针顺序排列的点,$ans$ 是这个凸包的面积。
