<h1>定义</h1>

又称单词查找树，字典树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。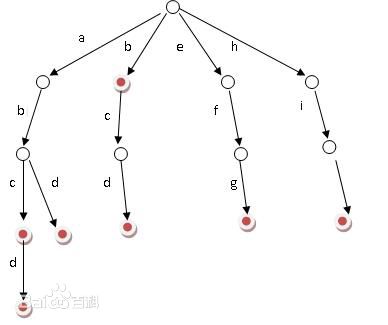

<h1>实现</h1>

首先我们以一道例题来看。

首先它给出了一个字符串集合，然后每次给出一个字符串询问有多少个字符串的前缀包含它。
如果暴力的话就会比较崩溃，这里我们可以使用一种优化。考虑暴力的时间瓶颈在于每次查询的时候必须从头开始重复计算，于是我们可以考虑用某种方式来把一些字符串相同的前缀合并起来表示，于是我们想到了树。
那么如何表示每一个单词呢？
我们把字母放在边上，如果这个节点是一个单词的结尾就打个标记就好了。
例如上图中的单词就有：abc,abd,abcd,b,bcd,efg,hi

<h2>结构体定义</h2>

struct Node{
    int val; // 自己根据题目记录的值
    Node *next[MAXM]; // MAXM 表示的字符集大小
}*root;

<h2>插入操作</h2>

void insert(char *str){
    Node *v = root;
    int len = strlen(str+1);
    FOR(i,1,len){
        int x = str[i] - 'a';
        // 如果这个地方没有出现过这个字符，就新建一个
        if(!v->next[x]) v->next[x] = New();
        v = v->next[x];
        // 进入下一层继续构建这个单词
        v->val++; // 根据前缀要求这里记录的是答案
    }
    // v->val++; // 如果是单纯查询单词的话
}

<h2>询问操作</h2>

int calc(char *str){
    int len = strlen(str+1);
    Node *v = root;
    FOR(i,1,len){
        int x = str[i]-'a';
        if(!v->next[x]) return 0; // 不存在这个前缀
        v = v->next[x];
    }
    return v->val; // 找到这个前缀了
}

总体来说还是十分通俗易懂的，trie 树的核心思想就是压缩数据规模，这样原来需要 $O(nm)$ 的复杂度被降到了 $O(size \times len)$ ，其中 $size$ 表示字符集大小，$len$ 表示字典中单词最大长度（即 trie 树最大深度）

<h1>题目练习</h1>

接下来我们来看一道变式题。
最长异或路径

<h2>题目描述</h2>

给定一棵 $n$ 个点的带权树，结点下标从 $1$ 开始到 $n$。寻找树中找两个结点，求最长的异或路径。
异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

<h2>解题报告</h2>

我们用 $\oplus$ 来表示异或。
首先发现异或有两个重要的性质：$a\oplus a = 0$,$a \oplus 0 = a$
所以我们发现询问两点之间的路径异或和相当于询问这两个点分别到根节点的异或和的异或值（因为 lca 到根的多余部分被重复异或抵消）。
一边 dfs 后问题转化为从一个序列中选择两个数使他们的异或和最大。
我们可以对所有数字按照从高位到低位的顺序建立一棵 01 trie 树，枚举第一个数，贪心的从二进制高位开始考虑第二个数，选择与当前这个数字二进制位不一样的路径走下去，最后取个 max 就可以了。

<h2>代码</h2>

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 100000+5;

struct Node{
    struct Edge *first;
    int dist;
}node[MAXN];

struct Edge{
    Node s,t;
    Edge *next;int w;
}pool[MAXN<<1],*frog = pool;

Edge New(Node s,Node *t,int w){
    Edge *ret = ++frog;
    *ret = (Edge){s,t,s->first,w};
    return ret;
}

inline void add(int u,int v,int w){
    node[u].first = New(&node[u],&node[v],w);
    node[v].first = New(&node[v],&node[u],w);
}

void dfs(Node v,Node fa=NULL){
    for(Edge *e = v->first;e;e = e->next){
        if(e->t == fa) continue;
        e->t->dist = v->dist^e->w;
        dfs(e->t,v);
    }
}

struct Trie{
    Trie *next[2];
}pool2[MAXN33],frog2 = pool2,*root;

Trie *New(){
    Trie *ret = ++frog2;
    ret->next[0] = ret->next[1] = NULL;
    return ret;
}

void insert(int x){
    Trie *v = root;
    ROF(base,30,0){
        int t = (x&(1<<base))>>base;
        if(!v->next[t]) v->next[t] = New();
        v = v->next[t];
    }
}

int query(int x){
    Trie *v=root;
    int ans = 0;
    ROF(base,30,0){
        int t = (x&(1<<base))>>base;
        // if(!v->next[0] && !v->next[1]) return 0;
        if(!v->next[!t]) v = v->next[t];
        else v = v->next[!t],ans += (1<<base);
    }
    return ans;
}

int N;

int main(){
    scanf("%d",&N);
    FOR(i,1,N-1){
        int u,v,w;scanf("%d%d%d",&u,&v,&w);
        add(u,v,w);
    }
    dfs(&node[1]);
    root = New();
    FOR(i,1,N) insert(node[i].dist);
    int ans = 0;
    FOR(i,1,N) ans = std::max(ans,query(node[i].dist));
    printf("%dn",ans);
    return 0;
}