<h1>输出方案</h1>

回忆前面我们解决二分图的方法：源点向每个左端节点连一个容量为 $1$ 的弧，每个右侧端点向汇点连一个容量为 $1$ 的弧，原图中的边容量为 $1$；所以说如果我们想获取方案的话我们只需要遍历左端点相连的弧是否满流即可。

<h2>交叉分组</h2>

建图方法显然，每个班级和每个小组都看成一个点。源点连向每个班级一条容量为 $a_i$ 的弧，每个小组连向汇点一条容量为 $b_i$ 的弧。之后对于每一个班级都连向所有的小组一条容量为 $1$ 的弧，最后判断最大流是不是等于总人数，如果是的话就输出即可。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 1000+5;
const int MAXM = 1000000+5;

struct Node{
    struct Edge first,cur;
    int level,num;
}node[MAXN];

struct Edge{
    Node s,t;
    Edge next,rev;
    int cap,flow;
}pool[MAXM<<1],*frog = pool;

Edge New(Node s,Node *t,int cap){
    Edge *ret = ++frog;
    *ret = (Edge){s,t,s->first,NULL,cap,0};
    return ret;
}

inline void add(int u,int v,int cap){
    node[u].first = New(&node[u],&node[v],cap);
    node[v].first = New(&node[v],&node[u],0);
    node[u].first->rev = node[v].first;
    node[v].first->rev = node[u].first;
}

int N,S,T;

bool bfs(Node s,Node t){
    FOR(i,0,N){
        node[i].cur = node[i].first;
        node[i].level = 0;
    }
    std::queue<Node *> q;q.push(s);
    s->level = 1;
    while(!q.empty()){
        Node *v = q.front();q.pop();
        for(Edge *e = v->first;e;e = e->next){
            if(e->flow < e->cap && !e->t->level){
                e->t->level = v->level + 1;
                if(e->t == t) return true;
                q.push(e->t);
            }
        }
    }
    return false;
}

int dfs(Node v,Node t,int limit=INT_MAX){
    int flow;
    if(v == t) return limit;
    for(Edge *&e = v->cur;e;e = e->next){
        if(e->flow < e->cap && e->t->level == v->level + 1)
            if((flow = dfs(e->t,t,std::min(limit,e->cap-e->flow)))){
                e->flow += flow;
                e->rev->flow -= flow;
                return flow;
            }
    }
    return 0;
}

int dinic(){
    int ret = 0,flow = 0;
    while(bfs(&node[S],&node[T])){
        while((flow = dfs(&node[S],&node[T]))) ret += flow;
    }
    return ret;
}

int n,m,sum;
int a[MAXN],b[MAXN];

int main(){
    scanf("%d%d",&n,&m);
    FOR(i,1,n) scanf("%d",a+i),sum += a[i];
    FOR(i,1,m) scanf("%d",b+i);
    S = 0,T = n+m+1;
    N = T;
    FOR(i,1,n) node[i].num = i;
    FOR(i,1,m) node[i+n].num = i;
    FOR(i,1,n) add(S,i,a[i]);
    FOR(i,1,m) add(n+i,T,b[i]);
    FOR(i,1,n) FOR(j,1,m) add(i,n+j,1);
    int ans=dinic();
    //DEBUG(ans);DEBUG(sum);
    if(ans != sum){
        puts("0");return 0;
    }
    puts("1");
    FOR(i,1,n){
        for(Edge *e = node[i].first;e;e = e->next){
            if(e->cap == e->flow)
                printf("%d ",e->t->num);
        }
        puts("");
    }
    return 0;
}

<h1>二分答案</h1>

在网络流题目中有一类题目可以归纳为“满足条件的最极值”的问题，需要用到二分答案然后建立网络流判断的问题，大体来说不难但是记住每次都要清空网络流防止爆炸。

<h1>拆点</h1>

一般拆点有两种情况：对点做限制或者根据题目描述有意义的进行拆分。我们重点来讲述一下第一类题目。
当我们对点有容量限制时，就需要把点拆成两个。对于下面这个网络：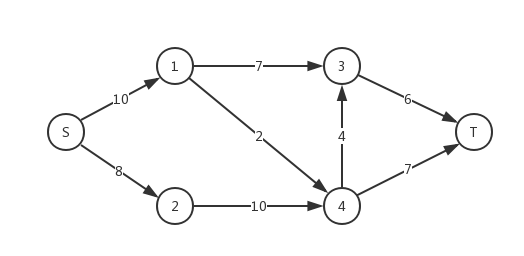

如果我们想限制所有点的流量不超过 $3$，我们可以对于每一个点 $u$ 都拆成 $u',u''$,将每条连入 $u$ 的点连入 $u'$，每条从 $u$ 连出的点改为由 $u''$ 连出，从 $u'$ 向 $u''$ 连一条容量为 $3$ 的弧。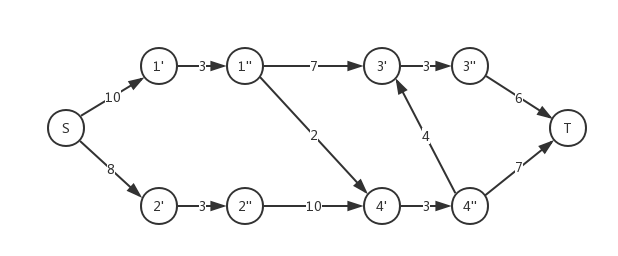
如果点有费用的话，只需要在拆点后的边加上费用就好了。

<h2>「BZOJ1738」</h2>

这是一道权限题题面可以从这里看：链接
题目大意：一张无向图，边有边权，现在每个点上有一定的奶牛，每个点有一个可以容纳奶牛的最大数字，这样其他的奶牛就要移动到其他的点上，求让所有奶牛都有地方容纳的最小距离。
我们先考虑判断是否能让所有奶牛都能被容纳：显然对于每个点可以容纳这个限制我们可以拆点，源点连向每个点的第一个点一条流量为牛的数量的弧，每个点的第二个点连向汇点一条流量为可以承受的牛的容量的弧，原图的边流量设为 $INF$ 即可。
显然现在我们可以枚举这个答案 $L$ ，首先 $O(n^3)$ 跑一边 Floyd 预处理点对距离，然后枚举点对距离 $\leq L$ 的建流量为 $INF$ 的弧。判断是否可行即可。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 2000 + 5;
const int MAXM = 500000 + 5;
#define int LL
struct Node{
    struct Edge first,cur;
    int level;
}node[MAXN];

struct Edge{
    Node s,t;
    Edge next,rev;
    int cap,flow;
}pool[MAXM<<1],*frog = pool;

inline void init(){
    CLR(pool,0);CLR(node,0);
    frog = pool;
}

Edge New(Node s,Node *t,int cap){
    Edge *ret = ++frog;
    *ret = (Edge){s,t,s->first,NULL,cap,0};
    return ret;
}

inline void add(int u,int v,int cap){
    // printf("%lld %lld %lldn",u,v,cap);
    node[u].first = New(&node[u],&node[v],cap);
    node[v].first = New(&node[v],&node[u],0);
    node[u].first->rev = node[v].first;
    node[v].first->rev = node[u].first;
}

int N,S,T;

bool bfs(Node s,Node t){
    FOR(i,0,N){
        node[i].cur = node[i].first;
        node[i].level = 0;
    }
    std::queue<Node *> q;
    q.push(s);s->level = 1;
    while(!q.empty()){
        Node *v = q.front();q.pop();
        for(Edge *e = v->first;e;e = e->next){
            if(e->flow < e->cap && !e->t->level){
                e->t->level = v->level + 1;
                if(e->t == t) return true;
                q.push(e->t);
            }
        }
    }
    return false;
}

int dfs(Node v,Node t,int limit=LLONG_MAX){
    if(v == t) return limit;
    int flow;
    for(Edge *&e = v->cur;e;e = e->next){
        if(e->flow < e->cap && e->t->level == v->level + 1){
            if((flow = dfs(e->t,t,std::min(limit,e->cap - e->flow)))){
                e->flow += flow;
                e->rev->flow -= flow;
                return flow;
            }
        }
    }
    return 0;
}

inline int dinic(){
    int flow,ans = 0;
    while(bfs(&node[S],&node[T])){
        while((flow = dfs(&node[S],&node[T]))){
            ans += flow;
        }
    }
    return ans;
}

LL fMAXN;
int a[MAXN],b[MAXN];
int n,m,sum;

inline void Floyd(){
    FOR(k,1,n){
        FOR(i,1,n){
            FOR(j,1,n){
                fi = std::min(fi,fi + fk);
            }
        }
    }
}

struct Data{
    int u,v,w;
}d[MAXM];

inline bool check(LL k){
    init();
    S = 0,T = 2*n+1;N = T;
    FOR(i,1,n) add(S,i,a[i]);
    FOR(i,1,n) add(i+n,T,b[i]);
    //FOR(i,1,n) add(i,i+n,b[i]);
    FOR(i,1,n) FOR(j,1,n){
        //if(i == j) continue;
        if(fi <= k) add(i,j+n,sum);//,printf("Link: %d %dn",i,j);
    }
    int ans = dinic();//DEBUG(ans);
    // BR;
    return (sum <= ans);
}

int line[MAXM],top = 0;
const int INF = 1000000000ll*MAXN;
signed main(){
    scanf("%lld%lld",&n,&m);
    LL L = 0,R = 0;
    FOR(i,1,n) FOR(j,1,n) fi = INF;
    //DEBUG(INF);
    FOR(i,1,n) fi = 0;
    FOR(i,1,n) scanf("%lld%lld",a+i,b+i);
    FOR(i,1,n) sum += a[i];
    // FOR(i,1,n) FOR(j,1,n) printf("%lld%c",fi,(j == n) ? 'n' : ' ');
    FOR(i,1,m){
        int u,v;LL w;
        scanf("%lld%lld%lld",&u,&v,&w);
        d[i] = (Data){u,v,w};
        fu = fv = std::min(fu,w);
        R += w;
    }
    Floyd();
    std::set<int> S;
    //FOR(i,1,n) FOR(j,1,n) printf("%lld%c",fi,(j == n) ? 'n' : ' ');
    FOR(i,1,n) FOR(j,1,n) if(fi != INF) S.insert(fi);
    for(std::set<int>::iterator it = S.begin();it != S.end();it++){
        line[++top] = *it;
    }
    LL ans = -1;
    L = 1,R = top;
    //DEBUG(check(70));
    while(L <= R){
        LL mid = (L+R)>>1;
        if(check(line[mid])) R = mid - 1,ans = mid;
        else L = mid + 1;
    }
    printf("%lldn",ans == -1 ? ans : line[ans]);
    return 0;
}

<h1>增加限制点</h1>

有时候我们希望对一组点或者总容量进行限制，这时候就要通过增加限制点来实现。
比如我们想在二分图匹配上增加一些限制：对于左侧集合的某些顶点，如 ${1,2,4}$，其中最多只能有 $2$ 的节点能在最终的匹配中。先来回顾一下二分图匹配相应的网络：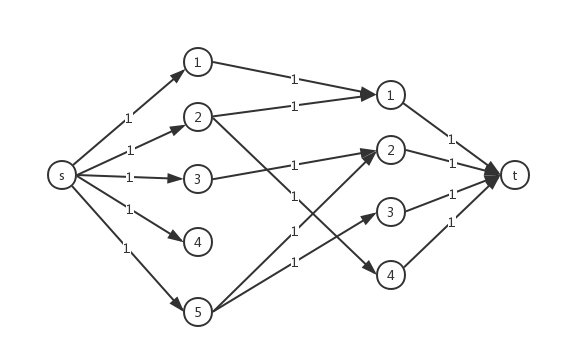

我们可以在源点和左侧顶点之间增加一个限制点：源点流入该点的弧容量为 $2$ ，该点连向 ${1,2,4}$ 这三个顶点。

这样就能确保 ${1,2,4}$ 至多有两个出现在最终的匹配方案中。