题目链接

<h1>题目描述</h1>

Emmy 在一个养猪场工作。这个养猪场有M个锁着的猪圈，但 Emmy 并没有钥匙。顾客会到养猪场来买猪，一个接着一个。每一位顾客都会有一些猪圈的钥匙，他们会将这些猪圈打开并买走固定数目的猪。 所有顾客有的钥匙和他们需要买猪的数量在事先都告诉了 Emmy，于是 Emmy 要订一个计划，使得卖出去的猪最多。 买卖的过程是这样的：一个顾客前来，并打开所有他可以打开的猪圈。然后 Emmy 从这些猪圈里牵出固定数目的猪卖给顾客（最多只能和顾客需要数相等），并可以重新安排这些开着的猪圈中的猪。 每个猪圈可以存放任意数目的猪。 写一个程序，使得 Emmy 能够卖出去尽可能多的猪。

<h2>输入样例</h2>

3 3
3 1 10
2 1 2 2
2 1 3 3
1 2 6

<h2>输出样例</h2>

7

<h1>解题报告</h1>

这是一道网络流题目，下面我来讲解一下如何建图。

• 三个顾客就有三轮交易，每一轮涉及到 $3$ 个猪圈和 $1$ 个顾客的节点
• 从源点到第一轮的各个猪圈各有一条边，容量就是各个猪圈里的猪的数量
• 从各个顾客到汇点有一个边，容量是购买上限
• 某一轮中从该顾客打开的所有猪圈都有一条边连向该顾客，容量为 $\infty $。
• 除了最后一轮从每一轮的第 $i$ 号猪圈连向下一轮表示猪可以留到下一轮
• 除了最后一轮每一轮被打开的所有猪圈到下一轮同样的猪圈两两连边，表明可以转换。
  (图源链接)

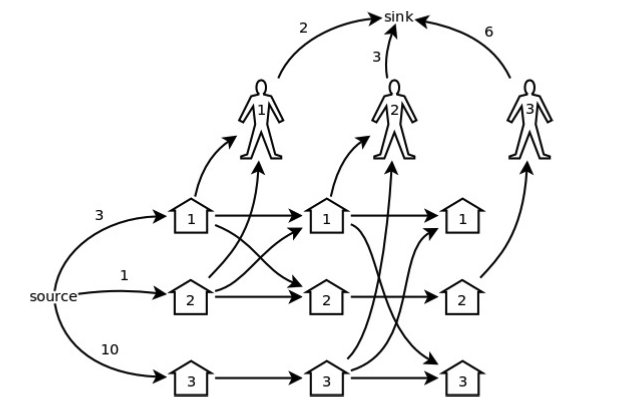
最大流即为答案。但是由于点和边太多导致根本跑不过去。让我们来考虑 合并/去除 无用点。
首先最后一轮没有打开的猪圈可以删除，也就是红色的，因为不会对答案造成任何影响。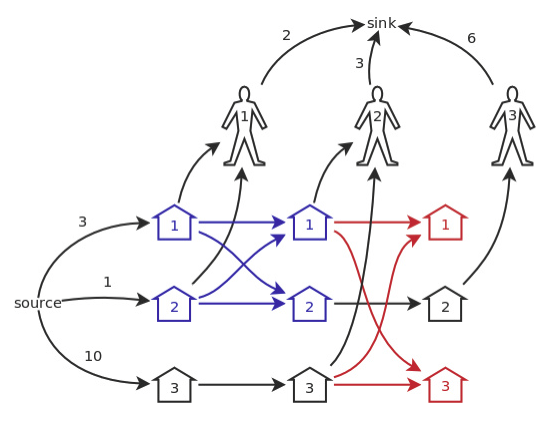

接着考虑蓝色部分，我们先来讲述一下什么情况下两个点可以合并。

1. 几个节点流量的来源完全相同，可以合并成一个。
2. 几个节点的去向完全相同，可以合并成一个。
3. 如果从点 $u$ 到点 $v$ 有一条流量为 $\infty$ 的边，并且点 $v$ 除了点 $u$ 没有其他的流量来源，可以合并成一个。
   我们按照这个规律来合并上图网络蓝色部分，初步得到了这个图：

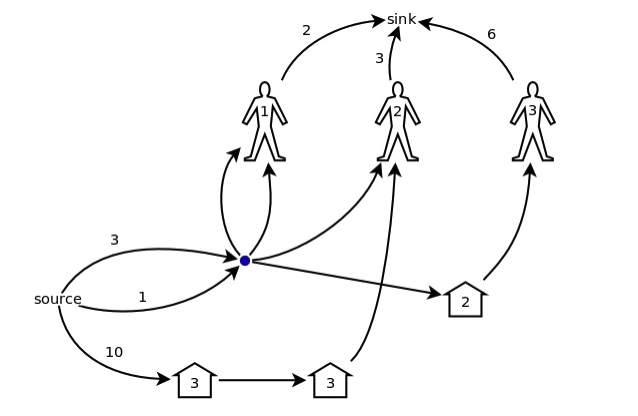
继续丧心病狂的合并，最终可以得到这个图：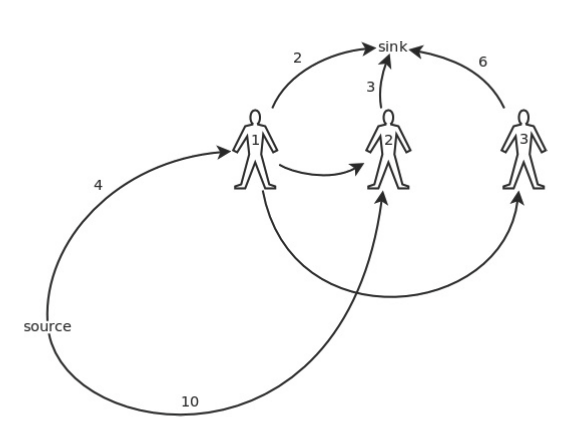
让我们来总结一下建图规律吧：

• 每个顾客都用一个节点来表示
• 对于每个猪圈的第一个顾客，从源点向他连一条边，容量为猪的初始数量，多条边可以合并，容量相加
• 对于每个猪圈，假设 $n$ 个顾客打开过它，则对于所有整数 $i \in [1,n) $，由 $i$ 向 $i+1$ 连容量为 $\infty$ 的边
• 从各个顾客向汇点连边，容量为顾客的购买上限

可以从该题中学到：遇到一个网络流题目如果没有思路的话，可以先建立一个最暴力朴素的网络流然后逐步优化无用点和边。

<h1>代码</h1>

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 10000+5;
const int MAXM = 1000000+5;

struct Node{
    struct Edge first,cur;
    int level;
}node[MAXN];

struct Edge{
    Node s,t;
    Edge next,rev;
    int cap,flow;
}pool[MAXM<<1],*frog = pool;

Edge New(Node s,Node *t,int cap){
    Edge *ret = ++frog;
    *ret = (Edge){s,t,s->first,NULL,cap,0};
    return ret;
}

inline void add(int u,int v,int cap){
    node[u].first = New(&node[u],&node[v],cap);
    node[v].first = New(&node[v],&node[u],0);
    node[u].first->rev = node[v].first;
    node[v].first->rev = node[u].first;
}

int N,S,T;

bool bfs(Node s,Node t){
    FOR(i,0,N){
        node[i].cur = node[i].first;
        node[i].level = 0;
    }
    std::queue<Node *> q;
    s->level = 1;q.push(s);
    while(!q.empty()){
        Node *v = q.front();q.pop();
        for(Edge *e = v->first;e;e = e->next){
            if(e->flow < e->cap && !e->t->level){
                e->t->level = v->level + 1;
                if(e->t == t) return true;
                q.push(e->t);
            }
        }
    }
    return false;
}

int dfs(Node v,Node t,int limit=INT_MAX){
    if(v == t) return limit;
    int flow;
    for(Edge *&e = v->cur;e;e = e->next){
        if(e->flow < e->cap && e->t->level == v->level + 1){
            if((flow = dfs(e->t,t,std::min(limit,e->cap-e->flow)))){
                e->flow += flow;
                e->rev->flow -= flow;
                return flow;
            }
        }
    }
    return 0;
}

inline int dinic(){
    int flow,ans = 0;
    while(bfs(&node[S],&node[T]))
        while((flow = dfs(&node[S],&node[T])))
            ans += flow;
    return ans;
}

int n,m;
int t[MAXN],fst[MAXN];

int main(){
    scanf("%d%d",&n,&m);
    FOR(i,1,n) scanf("%d",t+i);
    S = 0,T = m+1;N = T;
    FOR(i,1,m){
        int k,lim,sum=0;scanf("%d",&k);
        FOR(j,1,k){
            int x;scanf("%d",&x);
            if(!fst[x]) fst[x] = i,sum += t[x];
            else add(fst[x],i,INT_MAX);
        }
        scanf("%d",&lim);
        if(sum) add(S,i,sum);
        add(i,T,lim);
    }
    printf("%dn",dinic());
    return 0;
}