<h2>点双连通分量</h2>

点双连通图：如果一个无向图上没有割点，那么该图为点双连通图。显然有一个性质是同一个点双连通图中任意两点至少存在两条不经过重复点的路径。
点双连通分量：一个无向图的极大点双连通子图
我们可以使用 Tarjan 求解。
大家肯定都会无向图求割点了，我们其实只需要稍微改一下就可以了。
我们可以发现割点是两个点双的分割点，所以我们用栈来保存按照 $dfn$ 排序的目前还能进入新的点双里的非割点。
对于点 $u$ ，如果它的儿子 $v$ 满足 $low_v \geq dfn_u $，那么 $u$ 是割点，这时应不断退栈直到 $v$ 被弹出，那么弹出的所有点和 $u$ 形成一个点双。一个割点可以存在于多个点双中.

<h2>圆方树</h2>

圆方树是对于连通无向图定义的一颗树，其中每个原图中的点都叫圆点，而我们为每个点双都新建一个方点，而圆方树上所有边都是由一个方点和一个属于其对应点双的圆点相连这种形式。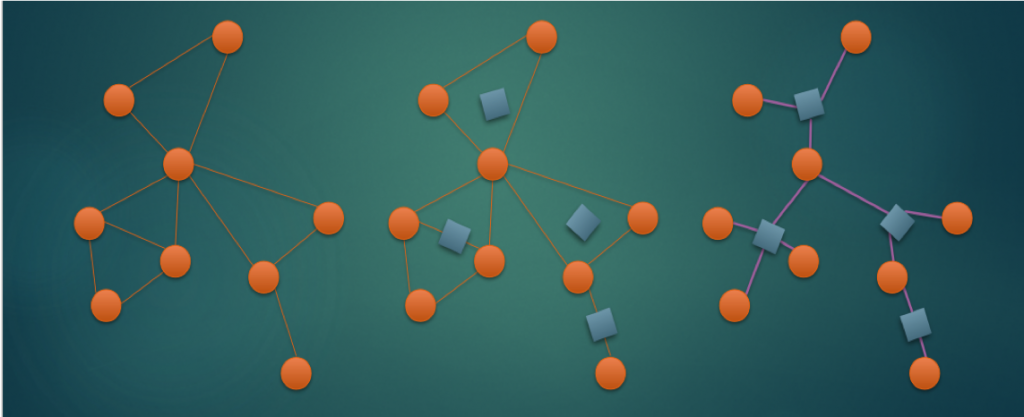

（第一个是原图，第三个是原图对应的圆方树）
不难发现圆方树有一些优美的性质，可以发现边只有从圆点连向方点的，任意圆点和方点间都没有边。
那么为什么这样构造的东西一定是一棵树呢？
注意树的一种定义形式：连通无环的无向简单图
连通显然，我们只需要证明无环。
考虑任意两个点双的交集，发现最多只有一个点（割点），那么就不可能存在环了。
但是这东西能用来做什么呢？我们来看一道例题。

<h2>「BZOJ3331」「BJOI2013」压力</h2>

题目描述
有一张 $n$ 个点 $m$ 条边的无向连通图，还有 $q$ 个点对，你需要输出每个点是多少给定点对的必经点（即如果点对为 $u,v$ ，那么如果 $u$ 到 $v$ 无论如何都要经过 $x$，那么 $x$ 是该点对的必经点）
$ 1\leq n \leq 10^5，1 \leq m,q \leq 2*10^5$

考虑直接建出圆方树，发现 $u,v$ 在圆方树路径上的圆点都是必经点，树上差分一下就可以了。
我们来考虑为什么这个结论是对的：考虑 $u,v$ 的可能路径一定跨过了若干个点双。对于每一个点双内的路径都存在至少两条不经过重复点的路径，对答案无贡献。也就是说对答案有贡献的只有起点终点和途径点双的交集点（即割点），那么体现在圆方树上就是路径上的所有圆点了。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 250000+5;
const int MAXM = 450000+5;

struct Edge{
    int to,next;
}e1[MAXM<<1],e2[MAXM<<1];
float log2N;
int head1[MAXN],head2[MAXN],cnt1,cnt2;
int dfn[MAXN],low[MAXN],bel[MAXN],st[MAXN],top;
int fMAXN,val[MAXN],tot,d[MAXN];
int N,M,Q;

inline void add1(int u,int v){
    e1[++cnt1] = (Edge){v,head1[u]};head1[u] = cnt1;
}

inline void add2(int u,int v){
    e2[++cnt2] = (Edge){v,head2[u]};head2[u] = cnt2;
}

void dfs1(int v){
    static int ts = 0;
    dfn[v] = low[v] = ++ts;st[++top] = v;
    for(int i = head1[v];i;i = e1[i].next){
        if(!dfn[e1[i].to]){
            dfs1(e1[i].to);low[v] = std::min(low[v],low[e1[i].to]);
            if(low[e1[i].to] >= dfn[v]){
                tot++;int t = -1;
                do{
                    t = st[top--];add2(tot,t);add2(t,tot);
                }while(t != e1[i].to);
                add2(tot,v);add2(v,tot);
            }
        }
        else low[v] = std::min(low[v],dfn[e1[i].to]);
    }
}

void dfs2(int v){
    FOR(i,1,log2N){
        if(d[v] <= (1<<i)) break;
        fv = ff[v][i-1];
    }
    for(int i = head2[v];i;i = e2[i].next){
        if(e2[i].to == fv) continue;
        f[e2[i].to][0] = v;
        d[e2[i].to] = d[v] + 1;
        dfs2(e2[i].to);
    }
}

int lca(int x,int y){
    int dx = d[x],dy = d[y];
    if(dx != dy){
        if(dx < dy) std::swap(x,y),std::swap(dx,dy);
        int d = dx - dy;
        FOR(i,0,log2N) if(d & (1<<i)) x = fx;
    }
    if(x == y) return x;
    ROF(i,log2N,0){
        if(fx == fy) continue;
        x = fx,y = fy;
    }
    return fx;
}

void dfs3(int v,int fa){
    // printf("%d %dn",v,fa);
    for(int i = head2[v];i;i = e2[i].next){
        if(e2[i].to == fa) continue;
        dfs3(e2[i].to,v);val[v] += val[e2[i].to];
    }
}

int main(){
    // freopen("1.in","r",stdin);
    // freopen("1.out","w",stdout);
    scanf("%d%d%d",&N,&M,&Q);tot = N;
    FOR(i,1,M){
        int u,v;scanf("%d%d",&u,&v);
        add1(u,v);add1(v,u);
    }
    log2N = log2(tot);
    FOR(i,1,N) if(!dfn[i]) dfs1(1);
    d[1] = 1;dfs2(1);
    FOR(i,1,Q){
        int x,y;scanf("%d%d",&x,&y);
        int l = lca(x,y);
        val[x]++;val[y]++;val[l]--;valf[l]--;
        //printf("%dn",l);
    }
    dfs3(1,0);
    FOR(i,1,N) printf("%dn",val[i]);
    return 0;
}