K-D Tree,全名k-dimensional Tree,是一种分割k维数据空间的数据结构。主要应用于多维空间关键数据的搜索(如:范围搜索和最近邻搜索)。K-D Tree是二进制空间分割树的特殊的情况,以下是一棵二维空间上的 k-d tree: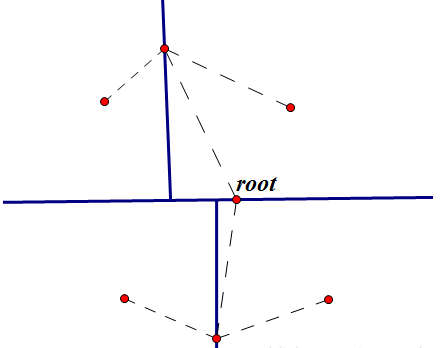
建树
K-D Tree 的建树过程类似于平衡树:对于已知点集,求出其在某一维度上排序后的中间点,作为这个空间的分割点,然后把空间一分为二,再对每个部分递归建树,返回子部分分割点的编号,作为当前部分分割点的左右儿子。关于每次按照哪个维度排序,最好的方案是按照方差大小,但是为了简便我们就遍历每一维来建立。
inline int build(int l,int r,int dir){
if(l > r) return 0;
int x = New(),mid = (l + r) >> 1;
nthdir = dir;
std::nth_element(data+l,data+mid,data+r+1);
p[x] = data[mid];lc = build(l,mid-1,dir^1);
rc = build(mid+1,r,dir^1);
pushup(x);return x;
}其中 pushup 函数维护了 max 和 min 两个数组,用来存储每一个分割空间的极值。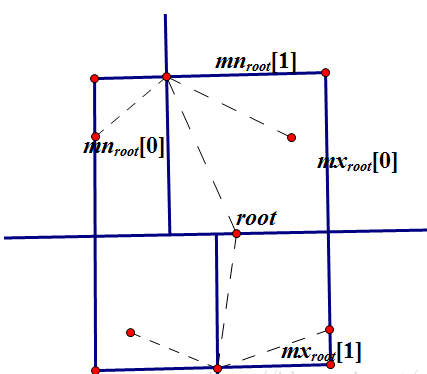
inline void pushup(int x){
FOR(i,0,1){
min[x][i] = max[x][i] = p[x][i];
if(lc){
min[x][i] = std::min(min[x][i],min[lc][i]);
max[x][i] = std::max(max[x][i],max[lc][i]);
}
if(rc){
min[x][i] = std::min(min[x][i],min[rc][i]);
max[x][i] = std::max(max[x][i],max[rc][i]);
}
}
size[x] = size[lc] + size[rc] + 1;
}插入
插入的时候就是从根开始,判断这个点在分割点的那边,如果有的话就递归插入子节点,否则直接创建新的子节点(也和平衡树很像)
删除和插入差不多......
inline void insert(int x,Point P,int dir){
if(P[dir] < p[x][dir]){
if(lc) insert(lc,P,dir^1);
else{
lc = ++cnt;p[cnt] = P;
min[cnt][0] = max[cnt][0] = P[0];
min[cnt][1] = max[cnt][1] = P[1];
}
}
else{
if(rc) insert(rc,P,dir^1);
else{
rc = ++cnt;p[cnt] = P;
min[cnt][0] = max[cnt][0] = P[0];
min[cnt][1] = max[cnt][1] = P[1];
}
}
pushup(x);
}查询
查询时对于每一个被分割的点集,先利用到分割点的距离更新答案,然后判断边界是否能用于更新答案,如果能的话,就递归进入这个子区域更新答案。为了提高效率,我们贪心的选择答案更优的地方优先递归查询。
inline void query(int x,Point P){
ans = std::min(ans,P-p[x]);
int L = INT_MAX,R = INT_MAX;
if(lc) L = calc(lc,P);
if(rc) R = calc(rc,P);
if(L < R){
if(L < ans) query(lc,P);
if(R < ans) query(rc,P);
}
else{
if(R < ans) query(rc,P);
if(L < ans) query(lc,P);
}
}例题:BZOJ2648
kdtree裸题。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define fi first
#define lc (ch[x][0])
#define se second
#define U unsigned
#define rc (ch[x][1])
#define Re register
#define LL long long
#define MP std::make_pair
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 1000000+5;
int min[MAXN][2],max[MAXN][2],ch[MAXN][2];
int nthdir;
inline void upmin(int &a,int b){
if(a > b) a = b;
}
inline void upmax(int &a,int b){
if(a < b) a = b;
}
struct Point{
int pos[2];
int& operator [](int x){
return pos[x];
}
bool operator < (const Point &t) const {
return pos[nthdir] < t.pos[nthdir];
}
int operator - (const Point &t) const {
return std::abs(pos[0]-t.pos[0]) + std::abs(pos[1]-t.pos[1]);
}
Point(int x,int y){
pos[0] = x;pos[1] = y;
}
Point(){}
}p[MAXN];
inline void pushup(int x){
if(lc){
upmin(min[x][0],min[lc][0]);
upmin(min[x][1],min[lc][1]);
upmax(max[x][0],max[lc][0]);
upmax(max[x][1],max[lc][1]);
}
if(rc){
upmin(min[x][0],min[rc][0]);
upmin(min[x][1],min[rc][1]);
upmax(max[x][0],max[rc][0]);
upmax(max[x][1],max[rc][1]);
}
}
inline int build(int l,int r,int dir){
nthdir = dir;int x = (l + r) >> 1;
std::nth_element(p+l,p+x,p+r+1);
min[x][0] = max[x][0] = p[x][0];
min[x][1] = max[x][1] = p[x][1];
if(l < x) lc = build(l,x-1,dir^1);
if(r > x) rc = build(x+1,r,dir^1);
pushup(x);return x;
}
int cnt;
inline void insert(int x,Point P,int dir){
if(P[dir] < p[x][dir]){
if(lc) insert(lc,P,dir^1);
else{
lc = ++cnt;p[cnt] = P;
min[cnt][0] = max[cnt][0] = P[0];
min[cnt][1] = max[cnt][1] = P[1];
}
}
else{
if(rc) insert(rc,P,dir^1);
else{
rc = ++cnt;p[cnt] = P;
min[cnt][0] = max[cnt][0] = P[0];
min[cnt][1] = max[cnt][1] = P[1];
}
}
pushup(x);
}
inline int calc(int x,Point P){
return std::max(0,min[x][0]-P[0]) + std::max(0,min[x][1]-P[1]) + std::max(0,P[0]-max[x][0]) + std::max(0,P[1]-max[x][1]);
} // 点 P 到分割集 x 的距离
int ans = INT_MAX;
inline void query(int x,Point P){
ans = std::min(ans,P-p[x]);
int L = INT_MAX,R = INT_MAX;
if(lc) L = calc(lc,P);
if(rc) R = calc(rc,P);
if(L < R){
if(L < ans) query(lc,P);
if(R < ans) query(rc,P);
}
else{
if(R < ans) query(rc,P);
if(L < ans) query(lc,P);
}
}
int N,M;
int main(){
//freopen("1.in","r",stdin);
scanf("%d%d",&N,&M);cnt = N;
FOR(i,1,N) scanf("%d%d",&p[i][0],&p[i][1]);
int root = build(1,N,0);
while(M--){
int opt,x,y;scanf("%d%d%d",&opt,&x,&y);
if(opt & 1) insert(root,Point(x,y),0);
else{
ans = INT_MAX;query(root,Point(x,y));
printf("%d\n",ans);
}
}
return 0;
}结语
其实 K-D Tree 更像是一种优化暴力的方法,他常数比较大,有时候为了防止被出题人构造数据卡,需要使用类似于替罪羊树的思想来不断调整树的平衡。

4 comments
orz 神wyh
wyh太强辣
Orz RainAir 一天学一个数据结构
您一天就学会了大部分省选数论内容 Orz
详情可以看他的博客:D