DDP（动态 dp），是通过将状态改写成矩阵，然后定义具有结合律的与转移等价的运算，用数据结构快速维护的一种方法。在 NOIP2018 时作为 Day2 T3 出现。
NOIP2018 Day2T3 - 保卫王国
考场上根本不会...那个时候我是连暴力 dp 都不会的菜鸡，现在回来学一学。
我们来找一道简单的题目入手：给定一棵树，点有点权，每次可以修改一个点的权值，每次修改后求这棵树的最大独立集。$n \leq 10^5$
如果这个问题是静态的，我们可以设出状态 $f_{i,0/1}$ ，表示以 $i$ 为根的子树内， $i$ 这个点是否选择时的最大权值和。转移显然：
$$f_{i,0} = \sum_{v \in son_i} max\{f_{v,0},f_{v,1}\}$$
$$f_{i,1} = \sum_{v \in son_i} f_{v,0}$$
我们观察在 dfs 中该 dp 的转移方式：我们发现这类 dp 对儿子的转移顺序 没有要求，所以我们可以先从轻儿子转移，再从重儿子转移。我们将这棵树重链剖分后，对于重链上的每一个点，我们记录从它所有轻儿子转移来的最好状态 $lf_{v,0/1}$，转移和上面的差不多，只需要限制不从重儿子转移就可以了。
于是假设我们先处理处理出 $lf$,然后观察 $lf$ 和 $f$ 之间的关系：发现如果想求重链上每一个点的 f 值，我们只需要将这个链抽出来跑序列 dp 就可以了，我们记重儿子为 $hson$,转移如下：
$$f_{i,0} = lf_{i,0}+max\{f_{hson,0},f_{hson,1}\}$$
$$f_{i,1} = lf_{i,1}+f_{hson,0}$$
于是我们对于链上的一段查询就变成了彻彻底底的区间查询了。我们考虑在修改一个点的时候，如果能快速维护对序列 dp 的修改操作，我们在这个点所在重链所在的线段树上进行修改操作，然后调到链的 $fa$ 上继续修改，就可以在 $O(log^2n)$ 的时间复杂度内完成这一操作。
现在问题就在于如何快速维护这一操作了。我们在维护一般的有加油乘的 dp 时，我们都是用矩阵乘法，这次我们考虑定义矩阵的广义乘法运算：
$$C_{i,j} = \max_{k=1}^n\{A_{i,k},B_{k,j}\}$$
我们发现这个运算具有结合律，所以可以在线段树上维护。
所以我们考虑这个简单的问题的转移写到矩阵上应该是：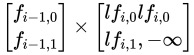

于是树剖后用线段树维护广义矩阵乘，就可以在 $O(nlog^2n)$ 的时间复杂度内做出本题。如果要追求 $O(nlogn)$ 的时间复杂度，可以使用 LCT 或者是全局平衡树来维护（虽然我都不会 zbl）。
贴一下代码：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdlib>
#include <cstdio>
#include <bitset>
#include <vector>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define fi first
#define se second
#define U unsigned
#define P std::pair
#define Re register
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
#define int LL
const int MAXN = 1e5 + 5;
int a[MAXN],n,m;
#define lc (x<<1)
#define rc (x<<1|1)
struct Matrix{
    LL a2;
    Matrix(){
        //FOR(i,0,1) FOR(j,0,1) ai = INT_MIN;
        CLR(a,0);
    }

    Matrix operator * (const Matrix &t) const {
        Matrix res;
        FOR(i,0,1){
            FOR(j,0,1){
                FOR(k,0,1) res.ai = std::max(res.ai,ai+t.ak);
            }
        }
        return res;
    }
}last,newm,val[MAXN],sm[MAXN<<2];

std::vector<int> G[MAXN];
int fa[MAXN],sz[MAXN],dep[MAXN],dfn[MAXN],edfn[MAXN],son[MAXN],tp[MAXN],id[MAXN];

inline void dfs1(int v,int faa=0){
    sz[v] = 1;fa[v] = faa;
    for(auto x:G[v]){
        if(x == faa) continue;
        dep[x] = dep[v] + 1;dfs1(x,v);
        sz[v] += sz[x];
        if(!son[v] || sz[son[v]] < sz[x]) son[v] = x;
    }
}

inline void dfs2(int v,int t=1,int fa=0){
    static int ts = 0;dfn[v] = ++ts;id[ts] = v;
    edfn[t] = ts;tp[v] = t;
    // if(v == son[fa]) tp[v] = t;
    // else tp[v] = v;
    if(son[v]) dfs2(son[v],t,v);
    for(auto x:G[v]){
        if(x == fa || x == son[v]) continue;
        dfs2(x,x,v);
    }
}

inline void split(int rt){
    dep[1] = 1;dfs1(rt);dfs2(rt);
}

int lfMAXN,fMAXN;

inline void dfs3(int v,int fa=0){
    lfv = a[v];
    for(auto x:G[v]){
        if(x == fa || x == son[v]) continue;
        dfs3(x,v);
        // upd lf
        lfv += std::max(fx,fx);
        lfv += fx;
    }
    fv += lfv;fv += lfv;
    if(!son[v]) return;
    dfs3(son[v],v);
    fv += std::max(f[son[v]][0],f[son[v]][1]);
    fv += f[son[v]][0];
}

inline void pushup(int x){
    sm[x] = sm[lc]*sm[rc];
}

inline void build(int x,int l,int r){
    if(l == r){
        val[id[l]].a0 = lf[id[l]][0];val[id[l]].a0 = lf[id[l]][0];
        val[id[l]].a1 = lf[id[l]][1];val[id[l]].a1 = -1e18;
        sm[x] = val[id[l]];
        return;
    }
    int mid = (l + r) >> 1;
    build(lc,l,mid);build(rc,mid+1,r);
    pushup(x);
}

inline Matrix query(int x,int l,int r,int L,int R){
    if(l == L && r == R) return sm[x];
    int mid = (l + r) >> 1;
    if(R <= mid) return query(lc,l,mid,L,R);
    if(L > mid) return query(rc,mid+1,r,L,R);
    return query(lc,l,mid,L,mid)*query(rc,mid+1,r,mid+1,R);
}

inline void update(int x,int l,int r,int pos){
    if(l == r && l == pos){
        sm[x] = val[id[pos]];return;
    }
    int mid = (l + r) >> 1;
    if(pos <= mid) update(lc,l,mid,pos);
    else update(rc,mid+1,r,pos);
    pushup(x);
}

inline void change(int v,int w){
    val[v].a1 += w - a[v];a[v] = w;
    while(v){
        int t = tp[v];
        last = query(1,1,n,dfn[t],edfn[t]);
        update(1,1,n,dfn[v]);
        newm = query(1,1,n,dfn[t],edfn[t]);
        v = fa[t];
        val[v].a0 += std::max(newm.a0,newm.a1)-std::max(last.a0,last.a1);
        val[v].a0 = val[v].a0;
        val[v].a1 += newm.a0 - last.a0;
    }
}

signed main(){
    scanf("%lld%lld",&n,&m);
    FOR(i,1,n) scanf("%lld",a+i);
    FOR(i,1,n-1){
        int u,v;scanf("%lld%lld",&u,&v);
        G[u].pb(v);G[v].pb(u);
    }
    split(1);dfs3(1);build(1,1,n);
    FOR(i,1,m){
        int x,y;scanf("%lld%lld",&x,&y);change(x,y);
        Matrix ans = query(1,1,n,dfn[1],edfn[1]);
        printf("%lldn",std::max(ans.a0,ans.a1));
    }
    return 0;
}

<h2>关于保卫王国</h2>

首先答案显然是全集-最大独立集，所以变成了最大独立集，每次钦定一些点是否选的问题。
我们可以让强制选的点设为一个极大值，最后在答案里减去就可以了。对于强制不选的点我们可以设为一个极小值，这样选了这个点一定不优就不会选。由于树剖常数比较大，所以我写了个 fread（
附代码（基本上差不多）：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdlib>
#include <cstdio>
#include <bitset>
#include <vector>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define fi first
#define se second
#define U unsigned
#define P std::pair
#define Re register
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

inline char nc(){
    #define SIZE 100000+5
    static char buf[SIZE],p1 = buf+SIZE,p2 = buf+SIZE;
    if(p1 == p2){
        p1 = buf;p2 = buf+fread(buf,1,SIZE,stdin);
        if(p1 == p2) return -1;
    }
    return *p1++;
}

inline void read(int &x){
    x = 0;char ch = nc();
    while(!isdigit(ch)) ch = nc();
    while(isdigit(ch)){
        x = (x<<1) + (x<<3) + (ch^'0');
        ch = nc();
    }
}

inline void read(LL &x){
    x = 0;char ch = nc();
    while(!isdigit(ch)) ch = nc();
    while(isdigit(ch)){
        x = (x<<1) + (x<<3) + (ch^'0');
        ch = nc();
    }
}

const int MAXN = 100000+5;
const LL MIN = -1e15;
std::vector<int> G[MAXN];
int n,m;LL a[MAXN];

#define lc (x<<1)
#define rc (x<<1|1)

struct Matrix{
    LL a2;
    Matrix(){CLR(a,0);}

    inline Matrix operator * (const Matrix &t) const {
        Matrix res;
        FOR(i,0,1){
            FOR(j,0,1){
                FOR(k,0,1) res.ai = std::max(res.ai,ai+t.ak);
            }
        }
        return res;
    }
}val[MAXN],sm[MAXN<<2],lst,now;

int fa[MAXN],dfn[MAXN],nfd[MAXN],id[MAXN],dep[MAXN],sz[MAXN],son[MAXN],tp[MAXN];
LL fMAXN,lfMAXN;

inline void dfs1(int v,int faa=0){
    fa[v] = faa;sz[v] = 1;
    for(auto x:G[v]){
        if(x == faa) continue;
        dep[x] = dep[v] + 1;dfs1(x,v);
        sz[v] += sz[x];
        if(!son[v] || sz[son[v]] < sz[x]) son[v] = x;
    }
}

inline void dfs2(int v,int t=1,int fa=0){
    static int ts = 0;dfn[v] = ++ts;nfd[t] = ts;
    id[ts] = v;tp[v] = t;
    if(son[v]) dfs2(son[v],t,v);
    for(auto x:G[v]){
        if(x == fa || x == son[v]) continue;
        dfs2(x,x,v);
    }
}

inline void dfs3(int v,int fa=0){
    lfv = a[v];
    for(auto x:G[v]){
        if(x == fa || x == son[v]) continue;
        dfs3(x,v);
        lfv += std::max(fx,fx);
        lfv += fx;
    }
    fv += lfv;
    fv += lfv;
    if(!son[v]) return;
    dfs3(son[v],v);
    fv += std::max(f[son[v]][0],f[son[v]][1]);
    fv += f[son[v]][0];
}

inline void pushup(int x){
    sm[x] = sm[lc]*sm[rc];
}

inline void build(int x,int l,int r){
    if(l == r){
        val[id[l]].a0 = lf[id[l]][0];val[id[l]].a0 = lf[id[l]][0];
        val[id[l]].a1 = lf[id[l]][1];val[id[l]].a1 = MIN;
        sm[x] = val[id[l]];return;
    }
    int mid = (l + r) >> 1;
    build(lc,l,mid);build(rc,mid+1,r);
    pushup(x);
}

inline Matrix query(int x,int l,int r,int L,int R){
    if(l == L && r == R) return sm[x];
    int mid = (l + r) >> 1;
    if(R <= mid) return query(lc,l,mid,L,R);
    if(L > mid) return query(rc,mid+1,r,L,R);
    return query(lc,l,mid,L,mid)*query(rc,mid+1,r,mid+1,R);
}

inline void update(int x,int l,int r,int pos){
    if(l == r && l == pos){
        sm[x] = val[id[pos]];
        return;
    }
    int mid = (l + r) >> 1;
    if(pos <= mid) update(lc,l,mid,pos);
    else update(rc,mid+1,r,pos);
    pushup(x);
}

inline void change(int v,LL w){
    //val[v].a1 += w-a[v];
    val[v].a1 += w;
    a[v] += w;
    while(v){
        int t = tp[v];
        lst = query(1,1,n,dfn[t],nfd[t]);
        update(1,1,n,dfn[v]);
        now = query(1,1,n,dfn[t],nfd[t]);
        v = fa[t];
        val[v].a0 += std::max(now.a0,now.a1) - std::max(lst.a0,lst.a1);
        val[v].a0 = val[v].a0;
        val[v].a1 += now.a0-lst.a0;
    }
}
LL sum = 0,xx;
std::set<int> S[MAXN];
signed main(){
    read(n);read(m);read(xx);DEBUG(xx);
    FOR(i,1,n) read(a[i]),sum += a[i];
    FOR(i,1,n-1){
        int u,v;read(u);read(v);
        G[u].pb(v);G[v].pb(u);S[u].insert(v);S[v].insert(u);
    }dep[1] = 1;
    dfs1(1);dfs2(1);dfs3(1);build(1,1,n);
    FOR(i,1,m){
        LL a,x,b,y;read(a);read(x);read(b);read(y);//scanf("%lld%lld%lld%lld",&a,&x,&b,&y);
        if(x == 0 && y == 0 && S[a].count(b)){
            puts("-1");continue;
        }
        x = x ? INT_MAX : INT_MIN;y = y ? INT_MAX : INT_MIN;
        x = -x;y = -y;
        change(a,x);change(b,y);
        Matrix res = query(1,1,n,dfn[1],nfd[1]);
        LL ans = std::max(res.a0,res.a1);
        printf("%lldn",sum-ans+std::max(x,0ll)+std::max(y,0ll));
        change(a,-x);change(b,-y);
    }
    return 0;
}