题目描述：给你若干条形如 $x+y=c$ 或 $x-y=c$ 的直线，这些直线与坐标轴的夹角是 45 度，问在矩形 $(0,0) \to (W,H)$ 中，有多少个子矩形。
图片示意：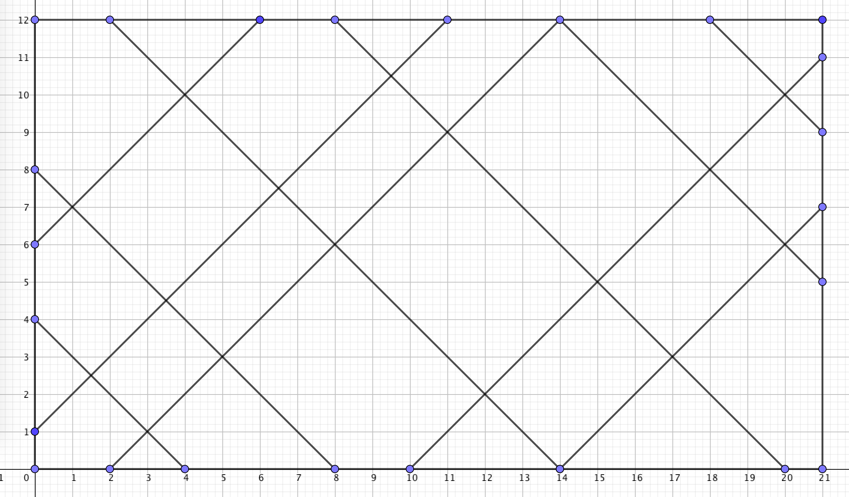

上图有 $19$ 个子矩形。
$n \leq 10^5$
首先这一题目 $O(n^3)$ 的复杂度十分好做：就是枚举三条边 去 map 找一下第四条边就好了。
我们考虑如何做到 $O(n^2logn)$:我们可以考虑先旋转坐标系，这样就是处理横着的和竖着的线了。
我们来考虑一下如何旋转坐标系：我们首先考虑将斜率为负的直线旋转到垂直方向上，那么斜率为正的直线就旋转到水平方向上了。考虑对于原来的一个点 $(x,y)$ ，旋转后变为 $\left(\frac{x+y}{\sqrt{2}},\frac{x-y}{\sqrt{2}}\right)$，但是我们发现有个$\sqrt{2}$很烦，所以我们令新坐标系的单位为 $\sqrt{2}$，旋转后的坐标也就是 $(x+y,x-y)$。
我们考虑枚举两条竖着的线，这样就能二分出有多少条横着的直线同时经过这两条竖线，记这样的横线的数量为 $a$，这两条竖线对答案的贡献就是 $\left(^a_2\right)$。
我们考虑如何在 $O(nlogn)$ 的时间内完成该题：考虑暴力枚举第 $i$ 条竖线后，记竖线 $i$ 和 $j$ 共同交的横线数量为 $cnt_{j}$，则我们需要统计：
$$\sum_{j = i+1}^n \left(^{cnt_{j}}_ 2\right)$$
我们考虑如何优化这个式子：我们先将竖线的 x 坐标和横线的左端点拿出来排序，然后使用扫描线思想，如果扫到了一条横线，那么在这条横线 $[l,r]$ 之间的所有竖线对的 $cnt$ 都会 $+1$，所以我们遇到横线就加一下前缀，然后对于竖线查询就需要快速统计一下上面的式子。
现在问题相当于转化为：需要实现一个数据结构 满足操作区间加，区间询问 $\sum_{i=l}^r \left(^{a_i}_ 2\right)$
我们对于线段树的每一个节点，维护区间和和组合数和。我们考虑单点 $+k$ 后对答案的贡献：
$$\left(^{x+k}_ 2\right) = \left(^x_2\right) + \left(^k_2\right) + xk$$
证明就是考虑组合意义，从 $x+k$ 个球中选出 $2$ 个，方案有全选 $[1,x]$ 之间的物品，全选 $[x+1,k]$，选一个 $[1,x]$ 和一个 $[x+1,k]$。
所以我们套个区间操作：

$$ \begin{aligned} \sum_ {i=l}^r \left(^{a_i+k}_ 2 \right) &= \sum_ {i=l}^ r \left(^{a_i}_ 2 \right)+k a_ i+\left(^k_ 2\right) \\ &=\sum_ {i=l}^r \left(^{a_ i}_ 2\right) + k\sum_ {i=l}^r a_ i + (r-l+1)\left(^k_ 2\right) \end{aligned} $$

所以维护区间和和区间组合数和，优先更新组合数就好了。
于是这个题就做完了。注意需要离散化+取模就可以了。

/*
 * Author: RainAir
 * Time: 2019-07-17 17:46:08
 */
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdlib>
#include <cstdio>
#include <bitset>
#include <vector>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define fi first
#define se second
#define U unsigned
#define P std::pair<LL,LL>
#define Re register
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

#define int LL
const int MAXN = 1e5 + 5;
const int ha = 1e9 + 7;
const int inv2 = 500000004;

inline void add(LL &a,LL b){
    a += b;while(a > ha) a -= ha;
    while(a < 0) a += ha;
}

int sm[MAXN<<2],cm[MAXN<<2],tag[MAXN<<2];
#define lc ((x)<<1)
#define rc ((x)<<1|1)

inline void pushup(int x){
    sm[x] = (sm[lc] + sm[rc])%ha;
    cm[x] = (cm[lc] + cm[rc])%ha;
}

inline void cover(int x,int l,int r,int k){
    (cm[x] += 1ll*(r-l+1)*k%ha*(k-1)%ha*inv2%ha + 1ll*sm[x]*k%ha)%=ha;
    (sm[x] += 1ll*(r-l+1)*k%ha) %= ha;
    add(tag[x],k);
}

inline void pushdown(int x,int l,int r){
    if(tag[x]){
        int mid = (l + r) >> 1;
        cover(lc,l,mid,tag[x]);
        cover(rc,mid+1,r,tag[x]);
        tag[x] = 0;
    }
}

inline void build(int x,int l,int r){
    tag[x] = 0;sm[x] = cm[x] = 0;
    if(l == r){
        return;
    }
    int mid = (l + r) >> 1;
    build(lc,l,mid);build(rc,mid+1,r);
    pushup(x);
}

inline void modify(int x,int l,int r,int L,int R,int k){
    if(L > R) return;
    if(l == L && r == R){
        cover(x,l,r,k);
        return;
    }
    int mid = (l + r) >> 1;pushdown(x,l,r);
    if(R <= mid) modify(lc,l,mid,L,R,k);
    else if(L > mid) modify(rc,mid+1,r,L,R,k);
    else modify(lc,l,mid,L,mid,k),modify(rc,mid+1,r,mid+1,R,k);
    pushup(x);
}

inline int query(int x,int l,int r,int L,int R){
    if(L > R) return 0;
    if(l == L && r == R) return cm[x];
    pushdown(x,l,r);
    int mid = (l + r) >> 1;
    if(R <= mid) return query(lc,l,mid,L,R);
    if(L > mid) return query(rc,mid+1,r,L,R);
    return query(lc,l,mid,L,mid)+query(rc,mid+1,r,mid+1,R);
}

int w,h,n,m;
int ans;
std::vector<P> t;
int v[MAXN],cnt;

signed main(){
    scanf("%lld%lld%lld%lld",&w,&h,&n,&m);
    FOR(i,1,n){
        int c;scanf("%lld",&c);
        v[++cnt] = c;t.pb(MP(c,INT_MAX));
    }
    std::sort(v+1,v+cnt+1);
    FOR(i,1,m){
        int d;scanf("%lld",&d);
        int p1 = std::abs(d);
        int p2 = std::min(2ll*h+d,2ll*w-d);
        // (w,w-c) (h+c,h)
        // (2w-c,-c) (2h+c,c)
        t.pb(MP(p1,p2));
    }
    std::sort(all(t));
    build(1,1,n);
    for(auto tt:t){
        int x = tt.fi,y = tt.se;
        if(y == INT_MAX){ // query
            int p = std::lower_bound(v+1,v+n+1,x)-v;
            if(p < n) (ans += query(1,1,n,p+1,n)) %= ha;
        }
        else{ // add
            int p = std::upper_bound(v+1,v+n+1,y)-v;p--; 
            if(p >= 1) modify(1,1,n,1,p,1);
        }
    }
    printf("%lld\n",ans);
    return 0;
}