网络流题目中,如果一种物品有两种状态(选或不选),告诉你每一种状态产生的收益/代价,我们就可以通过使用最小割模型来解决这个问题。但是如果物品的状态扩展到了 $k$ 种,我们就需要用一种新的建图方法。
我们拿两道题目举例:
<h3>RatingProgressAward</h3>
*TCO2017 Semifinal
题目链接
如果对于积分做了前缀和之后我们发现题目就是要求在满足限制的条件下最大化区间和。
对于一个点 如果我们知道了答案区间在哪 我们可以有三种状态:在答案区间左边,在大安区间内,在答案区间右边。这就是三种状态了。
我们发现在同一区间内 他们的顺序我们是不需要考虑的(内部顺序可以自己排),我们只需要考虑区间与区间的点是否满足拓扑图的要求。
首先对于每个点的三种状态,设积分为 $w$,我们设计出这样的网络:
如果割掉左边的边就会选择状态 1,后面同理。我们发现这个网络流就十分符合我们题目的要求。
然后我们考虑如何对点和点之间的限制。如果有一对限制 $(u,v)$ 表示 $u$ 要在前面,我们发现我们其实是不希望在第 $u$ 行上的割边在 $v$ 后面。所以我们只需要通过连容量为 $+\infty$ 的边来强制不能出现不符题意的情况即可。
建图大概如下: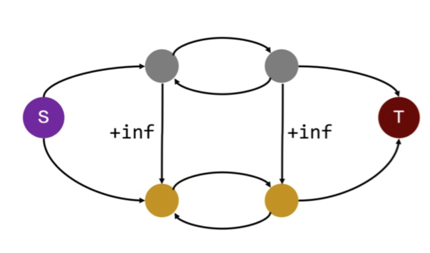
于是这个题目就可以愉快的写出代码了:
/*
* Author: RainAir
* Time: 2019-08-01 20:02:30
*/
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdlib>
#include <cstdio>
#include <bitset>
#include <vector>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define fi first
#define se second
#define U unsigned
#define P std::pair
#define Re register
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 200+5;
const int MAXM = MAXN*MAXN+2;
struct Edge{
int to,nxt,cap,flow;
}e[MAXM];
int head[MAXN],cur[MAXN],level[MAXN],cnt = 1;
int S,T,N;
inline void add(int u,int v,int w){
if(!w) return;
w = std::abs(w);//printf("%d %d %dn",u,v,w);
e[++cnt] = (Edge){v,head[u],w,0};head[u] = cnt;
e[++cnt] = (Edge){u,head[v],0,0};head[v] = cnt;
}
inline bool bfs(){
std::queue<int> q;
FOR(i,0,N) level[i] = 0,cur[i] = head[i];
q.push(S);level[S] = 1;
while(!q.empty()){
int v = q.front();q.pop();
for(int i = head[v];i;i = e[i].nxt){
if(!level[e[i].to] && e[i].cap > e[i].flow){
level[e[i].to] = level[v] + 1;
// DEBUG(e[i].to);
if(e[i].to == T) return true;
q.push(e[i].to);
}
}
}
return false;
}
inline int dfs(int v,int lim = INT_MAX){
if(!lim) return 0;
if(v == T) return lim;int flow;
for(int &i = cur[v];i;i = e[i].nxt){
if(e[i].cap > e[i].flow && level[e[i].to] == level[v] + 1){
if((flow = dfs(e[i].to,std::min(lim,e[i].cap-e[i].flow)))){
e[i].flow += flow;
e[i^1].flow -= flow;
return flow;
}
}
}
return 0;
}
inline int Dinic(){
int ans = 0,flow;
while(bfs()){
while((flow = dfs(S))) ans += flow;
}
return ans;
}
class RatingProgressAward{
public:
int n,m;
int maximalProgress(std::vector<int> change,std::vector<int> a,std::vector<int> b){
n = change.size();m = a.size();
S = 0,T = 2*n+1;N = T;int sm = 0;
FOR(i,1,n){
if(change[i-1] > 0) sm += change[i-1];
add(S,i,std::max(0,change[i-1]));
add(i,i+n,std::min(0,change[i-1]));
add(i+n,i,INT_MAX);
add(i+n,T,std::max(0,change[i-1]));
}
FOR(i,1,m){
add(b[i-1]+1,a[i-1]+1,INT_MAX);
add(b[i-1]+1+n,a[i-1]+1+n,INT_MAX);
}
return sm-Dinic();
}
};
<h3>FoxAndCity</h3>
*SRM590
题目链接
我们观察加入边之后的 $dis$ 数组,发现它需要满足以下条件:
- $dis_1 = 0,dis_i \neq 0(i \geq 2)$
- 对于原图中的边 $(u,v)$,满足 $|dis_u-dis_v| \leq 1$
- 设最长路径为 $k$,那么 $[0,k]$ 被 $dis$ 遍取。
我们发现从 $1,2$ 可以推出 $3$,所以我们只需要考虑满足 $1,2$ 限制。
我们首先发现一个点的 $dis$ 只有可能是 $[0,n-1]$,所以相当于是 $n$ 个不同的状态,并且代价也很好计算出来。
所以这个题的图就很好建出来了。。。沿用上一题的做法,边容量为这个点 $dis$ 为这个状态的时候对答案的贡献。
现在还有一个小问题:处理限制 $1$ 。
我们发现只需要让第一行强制选边 $0$ (边权为 $0$ 的状态容量为 $0$,其余容量为 $+\infty$),其余的点不允许选择边权为 $0$ 的状态(容量为 $+\infty$),然后直接跑网络流就可以了。
/*
* Author: RainAir
* Time: 2019-08-01 21:54:11
*/
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdlib>
#include <cstdio>
#include <bitset>
#include <vector>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define fi first
#define se second
#define U unsigned
#define P std::pair
#define Re register
#define LL long long
#define pb push_back
#define pw2(x) ((x)*(x))
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 500+5;
const int MAXM = 40000 + 5;
int mpMAXN;
struct Edge{
int to,nxt,cap,flow;
}e[MAXM<<2];
int cnt = 1,head[MAXM],level[MAXM],cur[MAXM];
inline void add(int u,int v,int w){
//if(v == 122) printf("%d %d %dn",u,v,w);
e[++cnt] = (Edge){v,head[u],w,0};head[u] = cnt;
e[++cnt] = (Edge){u,head[v],0,0};head[v] = cnt;
}
int S,T,N;
inline bool bfs(){
FOR(i,0,N) cur[i] = head[i];std::fill(level,level+N+1,0);
std::queue<int> q;q.push(S);level[S] = 1;
while(!q.empty()){
int v = q.front();q.pop();
// if(v >= 111) DEBUG(v);
for(int i = head[v];i;i = e[i].nxt){
// if(e[i].to == 122) DEBUG(level[e[i].to]);
// DEBUG(T);
if(!level[e[i].to] && e[i].cap > e[i].flow){
level[e[i].to] = level[v] + 1;
if(e[i].to == T) return true;
q.push(e[i].to);
}
}
}
return false;
}
inline int dfs(int v,int lim=INT_MAX){
if(v == T) return lim;
if(!lim) return 0;int flow;
for(int &i = cur[v];i;i = e[i].nxt){
if(e[i].cap > e[i].flow && level[e[i].to] == level[v]+1){
if((flow = dfs(e[i].to,std::min(lim,e[i].cap-e[i].flow)))){
e[i].flow += flow;
e[i^1].flow -= flow;
return flow;
}
}
}
return 0;
}
inline int Dinic(){
int ans = 0,flow;
while(bfs()){
// DEBUG(flow);
while((flow = dfs(S))) ans += flow;
}
return ans;
}
int n,m;
inline int calc(int x,int y){
return x+n*(y-1);
}
class FoxAndCity{
public:
int minimalCost(std::vector<std::string> linked, std::vector<int> want){
n = linked.size();m = want.size();
FOR(i,0,n-1){
FOR(j,0,n-1){
mpi+1 = linkedi == 'Y';
}
}
S = 0,T = n*n+1,N = T;//DEBUG(N);
// DEBUG(T);
FOR(i,1,n){
FOR(j,1,n){
if(j == 1) add(S,calc(i,j),i == 1 ? 0 : INT_MAX);
else add(calc(i,j-1),calc(i,j),i == 1 ? INT_MAX : pw2(want[i-1]-(j-1))),
add(calc(i,j),calc(i,j-1),INT_MAX);
}
add(calc(i,n),T,i == 1 ? INT_MAX : pw2(want[i-1]-n));
}
FOR(i,1,n){
FOR(j,1,i-1){
if(mpi == 1){
FOR(k,2,n){
add(calc(i,k),calc(j,k-1),INT_MAX);
add(calc(j,k),calc(i,k-1),INT_MAX);
}
}
}
}
return Dinic();
}
};

One comment
UPD: 第一题不用连反过来的 INF 边