<h2>C - Minimization</h2>
普及组题,不说了。
代码
<h2>D - Snuke Numbers</h2>
<h3>题意</h3>
将 $x$ 的数字和记作 $S(x)$。 称 $n$ 是好的,当且仅当 $\forall m>n, n \leq m$ 。
求第 $K$ 个好的数字。 保证答案不超过 $10^{15}$。
<h3>题解</h3>
全场最难的题。。。
我们设 $f(x)$ 表示满足 $\forall t>x ,\frac{t}{S(t)} \geq \frac{f(x)}{S(f(x))}$ 的数,那么答案就是通过多次迭代即可得出。
于是我们考虑如何求出 $f(x)$,打表可以找出规律:$f(x)$ 一定是通过将 $x$ 的后几位改成 $9$ 来实现的。
我们考虑如何证明它:设 $f(x)$ 从高往低第一位与 $x$ 不同的位置为 $d$。考虑如果存在 $t < d$,使得 $t$ 这一位不是 9,那我们将这一位改成 $9$,并将 $d$ 这一位减去 $1$,我们让新生成的这个数为 $g$,显然肯定有 $n < g \leq f(x)$,$S(g) > S(f(x))$,与 $f(x)$ 的定义矛盾。
然后证明 $f(x)$ 的 $10^d$ 是否是 $9$:我们考虑设这一位的数字加上一个 $t$(加上后这一位不会超过 $9$),那么权值是 $\frac{f(x)+k*10^d}{S(f(x))+k}$。找点特例画个图,发现是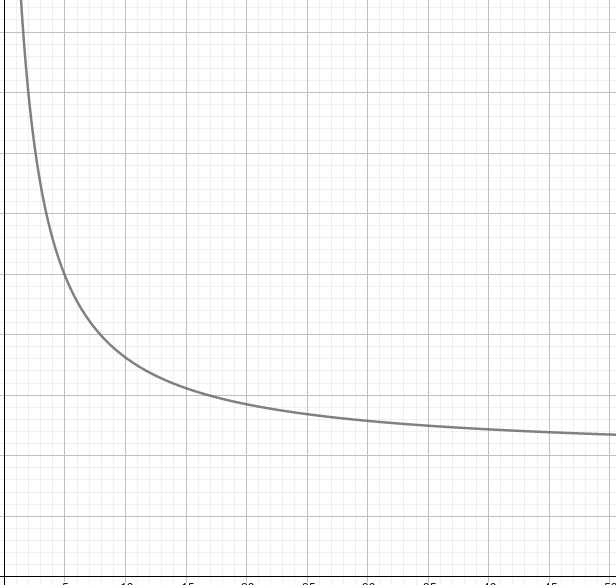
于是填成 $9$ 就是最优的了 QAQ。
所以我们求 $f(n)$ 就暴力枚举哪些位后面都是 $9$,都算一下权值找个最小的就好了。
代码
<h2>E - Independence</h2>
<h3>题目描述</h3>
给定 $N$ 的点 $M$ 条边无重边无自环无向图 $G$。 要你把所有点分成两半,使得每一半都是团。 在此基础上最小化两个团的边数之和。 $2\leq N\leq 700,0\leq M\leq N(N−1)$。
<h3>题解</h3>
这题目就简单多了
我们首先考虑对这个图求补图,原图的划分方案在补图上就对应了划分成了两个点集,点集之间两两无边,两点集之间可以有边。(其实就是个二分图)
我们唯一可以做的调整就是将一些连通块放置在某个点集中,我们先对每个连通块二分图染色,如果不能染则无解,那么我们先设 $a_i,b_i$ 表示第 $i$ 个连通块中白点和黑点的数目,显然白点不能和黑点在一块。然后直接设 $f_{i,j}$ 表示左边的点集大小为 $i$,右面的点集大小为 $j$ 是否能达成,直接转移就可以了。
代码
<h2>F - Eating Symbols Hard</h2>
<h3>题目描述</h3>
初始时有一个无限长初始为 $0$ 的序列 $A$ 和一个指针 $P = 0$,四种操作:
- +:$A_P + 1$
- -:$A_P − 1$
- >:$P + 1$
- <:$P − 1$
给定串 $S$,设执行完后 $A$ 数组的样子是 $B$,求 $S$ 有多少个非空子串操作完之后也是 $B$。
$1 \leq |S| \leq 2.5\times 10^5$。
<h3>题解</h3>
我们考虑如果求出来了 $h_i$ 表示执行完了 $1\text{~}i$ 操作得到的序列的 hash 值,那么就可以判断一个子区间$[l,r]$是否满足条件(设 hash 的 base 为$p$):$\frac{h_r-h_{l-1}}{p_{l-1}} = h_n$
移项可得 $h_r = h_np_{l-1}+h_{l-1}$
枚举一下 $l$,算算对应的 $r$ 有多少个就行了。
代码
