A
都相等就一个也消不掉,否则一定可以找到一个位置 $i$ 满足 $a_i$ 是最大值并且 $a_{i-1}$ 或 $a_{i+1}$ 有一个不是最大值(如果有定义的话),直接消成只剩一个即可。
B
考虑先做一次操作,序列就会同时包含 $0$ 和一个最大值 $x$,之后就是长度为 $2$ 的循环节了。
C
差分一下,变成每次选择一对 $l,r$ ,满足 $[l+1,r+1]$ 都 $>0$,可以让 $a_{r+1}-=1,a_l += 1$。考虑这里定义 $a_{n+1} = \infty$,所以相当于是差分序列的负值的绝对值的和。
D
考虑哪些形态是符合要求的:

也就是说最终肯定是若干个弱连通块,每个弱连通块一定是一对双向边连接两个点,然后还有最多两个点指向这两个双向边连接的点。
如果是一条长度为 $n$ 的链的话我们发现我们只需要 $\lceil \frac{n}{3}\rceil$ 次操作就能分成若干个这样的弱连通块了,所以答案就是对每一个弱连通块贪心一下,先找到这个双向边,保留左右最近的一个点,剩下的就是两条链。
E
考虑一条路径每个副对角线都会被恰好经过一次,对角线数量非常接近 $\log_2 10^{16}$,所以考虑我们构造使得在每个对角线上能知道它向下走还是向右走。
可以形如这样构造:
$$ \left[\begin{matrix} 0 & 0 & 0 &0&0\\ 2^0 & 2^1 & 2^2&2^3&\ldots\\ 0 & 0&0&\ldots&\ldots\\ 2^2&2^3&\ldots&\ldots&\ldots\\ 0&\ldots&\ldots&\ldots&\ldots \end{matrix}\right] $$
这样你在每一个位置向下和向右一定一个有值一个没值,然后每一个需要判断的地方获得的数都是不同位的。
这次比赛只能做到 E(应该是 Div1B)
F
首先最终的序列的差分序列一定只有 $0,1$
通过手玩或找规律可以发现最终的差分序列只会有至多一个位置是 $0$。
证明:首先我们发现操作的顺序和结果是无关的,然后我们每次可以加入一个数,执行以下操作:
假设当前在 $i$,如果 $a_{i-1}+2 < a_i$,就一直调整,然后令 $i-1 \to i$。否则直接停止。
我们发现这样一定保证了停止的时候前面一定都是已经不用调整的。
我们考虑如果现在 $i$ 前面没有相等的数,那么走完之后至多会产生一对相等的数(如果不在相等的地方停下来的话下一个又被减到不相等了);
如果 $i$ 前面有相等的数那么走完之后只会减少或者不变。因为走到相等的位置一定停下来,如果是形如 $x,x,x+2$ 的话数量就会不变,否则数量就会减一
综上所述:最终的序列的差分序列只会有至多一个位置是 $0$。
那么我们先设它没有位置是 $0$,设开头元素为 $h_1$,元素的和为 $s$,可以得到 $s=\frac{n(h_1+n-1)}{2}$。可以解出 $h_1$ ,这里注意上取整一下,然后就可以通过调整的方式来得到想要的解了。因为你调整可以减少的区间一定是 $[0,n-1]$,发现你最后是一个 $\frac{???}{n}$,所以它一定能被调整好。
G
这题我们想的方向一定是如何快速算一个区间的答案。
先约定一个记号:对字符串 $s$ 操作 $[a \to b]$ 表示从 $a$ 操作到 $b$(有可能 $a > b$,这时候的意思是倒着来)
首先我们观察一个显然的事实:如果 $s$ 和 $t$ 同时交换相同的位置,相同的位置的个数是不变的。
那么我们设对 $s$ 操作 $[l \to r]$ 得到字符串 $s'$,设对 $s$ 操作 $[l-1 \to 1]$ 得到 $s''$,对 $t$ 操作 $[r \to 1]$ 得到 $t''$,我们发现 $s'$ 和 $t$ 的相同位置的个数就等于 $s''$ 和 $t''$ 的相同位置的操作个数。(这里要倒过来的原因是我们是反过来对 $t$ 操作的)
那么我们可以设 $s_i$ 表示 $s$ 操作 $[i \to 1]$ 后得到的结果,$t_i$ 表示 $t$ 操作 $[i \to 1]$ 得到的结果,区间 $[l,r]$ 的答案就是 $s_{l-1}$ 和 $t_r$ 相同位置的个数。
但这样做还是 $n^2$ 的,我们观察另一个性质:设两个串 $s,t$ 长度为 $k$ 相同位置个数的数量为 $\omega$,$s$ 中 $1$ 的个数为 $\alpha$,$t$ 中 $1$ 的个数为 $\beta$,$s,t$ 中同时为 $1$ 的位置个数为 $\epsilon$,同时为 $0$ 的位置个数为 $\zeta$ 我们可以发现:
$$ \begin{aligned} \omega &= \epsilon+\zeta\\ &=\epsilon+k-\alpha-\beta+\epsilon\\ &=2\epsilon+k-\alpha-\beta \end{aligned} $$
而我们的操作都是交换,所以 $k,\alpha,\beta$ 都是定值,我们相当于要最大化 $s \text{ and } t$ 的 $1$ 的数量(满足区间长度限制前提下)
这个就可以预处理出 $f_S,g_S$ 表示 $S$ 以及 $S$ 的超集可以取到最小的 $l$ 和最大的 $r$,判断一下就好了。
I
先考虑如何做单组询问。
首先我们可以考虑只保留 $\geq x$ 的点,相邻点连边建出一个图 $G_1$, $<x$ 的点建出 $G_2$。
显然这两个点都是平面图,于是就有
$V_1-E_1+F_1 = C_1+1$
$V_2-E_2+F_2=C_2+1$
我们发现 $G_1$ 中大部分面都是 $G_2$ 中一个 bad 的联通块,除了这种情况:
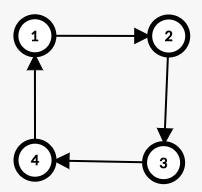
中间没有任何点,我们设 $G_1,G_2$ 中形如这样的四元环的个数为 $Q_1,Q_2$。
设 $G_1,G_2$ 中 bad 的连通块个数分别为 $C'_1,C'_2$
可以发现
$C'_1 = F_2-Q_2$
$C'_2 = F_1-Q_1$
由于点和边和环我们比较好统计,面和连通块不太会统计,考虑把答案表示成点边环的形式:
首先把上面两个欧拉定理得到的式子相减可以得到:
$$ C_1-C_2-F_1+F_2 = V_1-E_1-V_2+E_2 $$
于是代入可以得到:
$$ \begin{aligned} \text{ans} &= C_1+C'_1-C_2-C'_2 \\ &= C_1+F_2-Q_2-C_2-F_1+Q_1\\ &= V_1-E_1-V_2+E_2+Q_1-Q_2 \end{aligned} $$
算边我们可以考虑拆开算横向边和纵向边。我们这里只举一个 $ \geq x$,算横向边的例子。
一个边合法当且仅当:
$a_i+b_j \geq x,a_i+b_{j+1} \geq x$
也就是 $a_i + \min\{b_j,b_{j+1}\} \geq x$
那么我们设 $B_i = \min\{b_i,b_{i+1}\}$
那么就是 $a_i+B_j \geq x$ 的对数,可以 NTT 卷积一下。
