题目太水了，是手速场。

A

如果 $a,b,c,d,e,f > 0$，那么就是判断转换效率是否 $>1$，也就是 $\frac{bdf}{ace}>1 \Rightarrow bdf > ace$。

但是会有 $0$ 的情况，我们发现我们需要特判 $c=0,d \neq 0$ 和 $a=0,b,d \neq 0$ 的情况，剩下的情况都能用上式判断。

#include <bits/stdc++.h>

#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

int main(){
    // freopen("A.in","r",stdin);
    // freopen("A.out","w",stdout);
    int T;scanf("%d",&T);
    while(T--){
        LL a,b,c,d,e,f;scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&e,&f);
        // *b*d*f > e*c*a
        if(c == 0 && d != 0){
            puts("MEI");
            continue;
        }
        if(a == 0 && b != 0 && d != 0){
            puts("MEI");
            continue;
        }
        puts(b*d*f > e*c*a ? "MEI":"FON");
    }
    return 0;
}

B

考虑倒着做求出每个操作被执行了多少次，一个操作 $2$ 相当于将区间内的操作次数都加上这个操作的操作次数，由于操作和询问都是单调向前的，所以可以用差分解决。

然后操作 $1$ 也可以用差分解决。

#include <bits/stdc++.h>

#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 2e5 + 5;
const int ha = 1e9 + 7;

inline void add(int &x,int y){
    x += y;if(x >= ha)x -= ha;
}
int n,q;

int opt[MAXN],l[MAXN],r[MAXN];
int cf[MAXN],ans[MAXN];

int main(){
    scanf("%d%d",&n,&q);
    FOR(i,1,q) scanf("%d%d%d",opt+i,l+i,r+i);
    int now = 1;
    ROF(i,q,1){
        add(now,cf[i]);
        // DEBUG(now);
        if(opt[i] == 1){
            add(ans[l[i]],now);
            add(ans[r[i]+1],ha-now);
        }
        else{
            add(cf[l[i]-1],ha-now);
            add(cf[r[i]],now);
        }
    }
    FOR(i,1,n) add(ans[i],ans[i-1]);
    FOR(i,1,n) printf("%d%c",ans[i]," \n"[i==n]);
    return 0;
}

C

考虑斯特林公式：

$$ \begin{aligned} \sum_{S \subseteq V} f(S)^k = \sum_{i=0}^k \left\{^k_i\right\} f(S)^{\underline k} \end{aligned} $$

所以相当于要对于 $k=1\ldots 3$，计算出从所有图中有序选出 $k$ 条边的方案数。

我们枚举这个边的 $k$ 元组，相当于要计算有多少个图包含它，设这个组总共有 $x$ 个端点，那么方案数就是 $2^{n-x}$。所以我们相当于要对所有可能的点数都计数。

发现 $k=1$ 时，答案就是 $m2^{n-1}$。

发现 $k=2$ 时，情况只有一条长度为 $2$ 的链（长度表示边数）和两个端点不交的边，点数分别是 $3,4$。链可以通过枚举中心点解决，剩下那种情况可以容斥。

发现 $k=3$ 是，情况有五种：

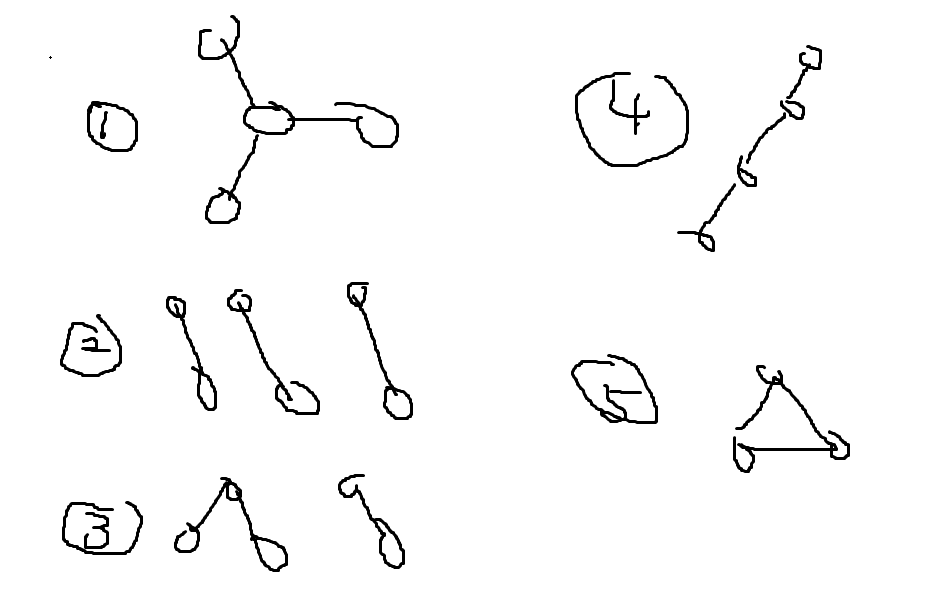
分别计算即可。

具体说一下我是咋算的：首先情况 $5$ 就是三元环计数，将边重定向为度数小的点向度数大的点连边，如果度数相同就按照编号连边，然后对于每个点，暴力遍历能到达的点打标记，再暴力遍历能到达的点的相邻的点，有标记答案就加一，复杂度是 $O(m\sqrt m)$ 的。

然后情况 $4$ 我们考虑枚举与端点距离为 $1$ 的点，然后先算出来以这个为中心的长度为 $2$ 的链有多少个，对于每种可能我们都随便选某个端点的相邻的边作为另一条边，设点的度数为 $deg_v$，那么答案就是

$$ \sum_{x=1}^m \sum_{y=x+1}^m (deg_x+deg_y-2) = \sum_{x=1}^m (deg_v-1)(deg_x-1) $$

就可以 $O(m)$ 的去算了，但是会多算情况 $5$，对于每一个三元环都会被算 $6$ 遍，减去后发现每条链都会被算 $2$ 遍。

情况 $1$ 就是 $\sum_i \binom {deg_i}{3}$。

情况 $3$ 可以先枚举长度为 $2$ 的链的中心，然后要求第三条边不能和中心相连，发现这样可能多算了 $3$ 遍三元环，和 $2$ 遍长度为 $3$ 的链，减掉就行。

补集转化就可以算出情况 $2$，对应加起来就行。

注意这里斯特林公式不能直接加上 $k=2$ 的答案。。需要加恰好选两条不同边的方案。。

#pragma GCC optimize("Ofast")
#include <bits/stdc++.h>

#define fi first
#define se second
#define db double
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 1e5 + 5;
const int ha = 1e9 + 7;
const int inv2 = 500000004;

inline char nc(){
    #define SIZE 1000000+3
    static char buf[SIZE],*p1 = buf+SIZE,*p2 = buf+SIZE;
    if(p1 == p2){
        p1 = buf;p2 = buf+fread(buf,1,SIZE,stdin);
        if(p1 == p2) return -1;
    }
    return *p1++;
    #undef SIZE
}

template <typename T>
inline void read(T &x){
    x = 0;int flag = 0;char ch = nc();
    while(!isdigit(ch)){
        if(ch == '-') flag = 1;
        ch = nc();
    }
    while(isdigit(ch)){
        x = (x<<1) + (x<<3) + (ch^'0');
        ch = nc();
    }
    if(flag) x = -x;
}

struct Edge{
    int u,v;
    Edge(int u=0,int v=0) : u(u),v(v) {}
}e[MAXN];
int n,m,k;
int fac[MAXN],inv[MAXN],pw[MAXN];

inline int qpow(int a,int n=ha-2){
    int res = 1;
    while(n){
        if(n & 1) res = 1ll*res*a%ha;
        a = 1ll*a*a%ha;
        n >>= 1;
    }
    return res;
}

inline void prework(){
    fac[0] = 1;FOR(i,1,MAXN-1) fac[i] = 1ll*fac[i-1]*i%ha;
    inv[MAXN-1] = qpow(fac[MAXN-1]);ROF(i,MAXN-2,0) inv[i] = 1ll*inv[i+1]*(i+1)%ha;
    pw[0] = 1;FOR(i,1,MAXN-1) pw[i] = 2ll*pw[i-1]%ha;
}

inline int C(int n,int m){
    if(n < 0 || m < 0 || n < m) return 0;
    return 1ll*fac[n]*inv[m]%ha*inv[n-m]%ha;
}

inline void add(int &x,int y){
    x += y;if(x >= ha) x -= ha;
}

namespace BF{
    int cnt[MAXN],now;

    inline bool check(){
        return n <= 300 && m <= 300;
    }

    inline void ins(int x){
        if(!cnt[x]) now++;
        ++cnt[x];
    }

    inline void del(int x){
        if(cnt[x] == 1) now--;
        --cnt[x];
    }

    int ans,cc = 0;
    int vis[MAXN];

    inline void dfs(int step,int fg=0){
        if(step == k+1){
            add(ans,pw[n-now]);
            return;
        }
        FOR(i,1,m){
            ins(e[i].u);ins(e[i].v);
            vis[i]++;
            dfs(step+1,fg+(vis[i]==1));
            vis[i]--;
            del(e[i].u);del(e[i].v);
        }
    }

    inline void Solve(){
        dfs(1);
        printf("%d\n",ans);
        // DEBUG(cc);
        exit(0);
    }
}

namespace Subtask1{
    inline bool check(){
        return k == 1;
    }

    inline int Solve(){
        return 1ll*m*pw[n-2]%ha;
    }
}

int deg[MAXN];

namespace Subtask2{
    inline bool check(){
        return k == 2;
    }

    inline int Solve(){
        int gx1 = 0;
        FOR(i,1,m) add(gx1,m-deg[e[i].u]-deg[e[i].v]+1);
        int gx2 = 1ll*m*(m-1)%ha;
        add(gx2,ha-gx1);
        int ans = 0;
        add(ans,1ll*gx1*pw[n-4]%ha);
        add(ans,1ll*gx2*pw[n-3]%ha);
        add(ans,1ll*m*pw[n-2]%ha);
        return ans;
    }
}

namespace Subtask3{
    inline bool check(){
        return k == 3;
    }

    std::vector<int> G[MAXN];
    int gx0,gx1,gx2,gx3,gx4;
    bool vis[MAXN];

    inline int gao(){
        int res = 0;
        FOR(u,1,n){
            for(auto v:G[u]) vis[v] = 1;
            for(auto v:G[u]) for(auto w:G[v]) if(vis[w]) res++;
            for(auto v:G[u]) vis[v] = 0;
        }
        return res;
    }

    inline int Solve(){
        FOR(i,1,m){
            if(e[i].u > e[i].v) std::swap(e[i].u,e[i].v);
            if(deg[e[i].u] <= deg[e[i].v]) G[e[i].u].pb(e[i].v);
            else G[e[i].v].pb(e[i].u);
        }
        gx0 = gx1 = gx2 = gx3 = gx4 = 0;
        FOR(i,1,n) add(gx0,C(deg[i],3));
        gx4 = gao();
        FOR(i,1,n) G[i].clear();
        FOR(i,1,m) G[e[i].u].pb(e[i].v),G[e[i].v].pb(e[i].u);
        FOR(v,1,n){
            int s = 0;
            for(auto x:G[v]) add(s,deg[x]-1);
            s = 1ll*s*(deg[v]-1)%ha;
            add(gx3,s);
        }
        add(gx3,ha-6ll*gx4%ha);
        gx3 = 1ll*gx3*inv2%ha;
        FOR(v,1,n){
            int s = 1ll*C(deg[v],2)*(m-deg[v])%ha;
            add(gx2,s);
        }
        add(gx2,ha-3ll*gx4%ha);
        add(gx2,ha-2ll*gx3%ha);
        gx1 = C(m,3);
        add(gx1,ha-gx0);
        add(gx1,ha-gx2);
        add(gx1,ha-gx3);
        add(gx1,ha-gx4);
        int ans = 0;
        if(gx0) add(ans,1ll*gx0*pw[n-4]%ha);
        if(gx1) add(ans,1ll*gx1*pw[n-6]%ha);
        if(gx2) add(ans,1ll*gx2*pw[n-5]%ha);
        if(gx3) add(ans,1ll*gx3*pw[n-4]%ha);
        if(gx4) add(ans,1ll*gx4*pw[n-3]%ha);
        ans = 1ll*ans*fac[3]%ha;
        add(ans,3ll*Subtask2::Solve()%ha);
        add(ans,ha-2ll*Subtask1::Solve()%ha);
        return ans;
    }
}

std::mt19937 g(time(NULL));
std::map<P,int> S; 

int main(){
    prework();
    read(n);read(m);read(k);
    // FOR(i,1,m) ++deg[e[i].u],++deg[e[i].v]; 
    FOR(i,1,m) read(e[i].u),read(e[i].v),++deg[e[i].u],++deg[e[i].v];
    if(BF::check()) BF::Solve();
    else if(Subtask1::check()) printf("%d\n",Subtask1::Solve());
    else if(Subtask2::check()) printf("%d\n",Subtask2::Solve());
    else if(Subtask3::check()) printf("%d\n",Subtask3::Solve());
    return 0;
}