Dinic 是一种网络最大流的算法。
<h1>引入</h1>
网络流的本质是线性规划。
定义:有向图 $(V,E)$ 存在源点 $S \in V$ 和汇点 $T \in V,S \neq T$,每条边都有一个容量 $c$。
对于任意一个时刻,设 $flow(u,v)$ 表示实际流量,则整个图 $G$ 的流网络满足如下性质:
- 容量限制:$\forall u,v $,$flow(u,v) < c(u,v)$
- 反对称性: $\forall u,v $,存在 $ flow(u,v) = -flow(v,u) $
- 流量平衡, $\forall u,u \neq S,u \neq T$,应满足 $\sum flow(u,v) = 0$,即每个点不会制造或消耗流量。
可行流:在容量网络 G 中满足以下条件的网络流 flow ,称为可行流. - 弧流量限制条件: $0 \leq flow(u,v) \leq c(u,v)$
- 平衡条件: 即流入一个点的流量要等于流出这个点的流量(源点和汇点除外).
零流:如果网络流上每条弧的流量都为 $0$ ,则该网络流成为零流。
伪流:如果一个网络流只满足弧流量限制条件,不满足平衡条件,则这种网络流为伪流,或称为容量可行流.(预流推进算法有用)
在容量网络中,满足弧流量限制条件,且满足平衡条件并且具有最大流量的可行流,称为网络最大流,简称最大流.
残余流量:可以感性理解为 $cl(u,v) = c(u,v) - flow(u,v)$
残余网络:在一个网络流图上,找到一条源到汇的路径后,对路径上所有的边,其容量都减去此次找到的量,对路径上所有的边,都添加一条反向边,其容量也等于此次找到的流量,这样得到的新图,就称为原图的残余网络。
上面讲了一些基本的定义,看完下面的内容已经足够了。
<h1>Dinic</h1>
<h2>增广路找最大流</h2>
首先注意一个性质:如果一个可行流不是最大流,那么当前网络中一定存在一条增广路。(作者也不会证明)
增广路大家在学习二分图的时候一定都听说过了。
大概找增广路的过程就是 dfs 一遍,判断这条边残量是否大于 $0$,如果大于 $0$ 就通过这条边进行增广。
详细说一下找增广路的过程:
- 找到一条从源点到汇点的路径,使得路径上每一条边的残留都 $>0$,这条路径叫做增广路;
- 找到这条路径上最小的残量,记为 $f$;
- 将这条路径上每一条有向边的残量减去 $f$,同时对于反向边的残量加上 $f$;
- 重复直到找不到增广路。
<h2>为什么要建反向边</h2>
因为你在寻找增广路的时候,在前面找到的不一定是一个最优解,如果我们建一个流量相反的边,那么就代表可以从这条反向边流过而实现反悔。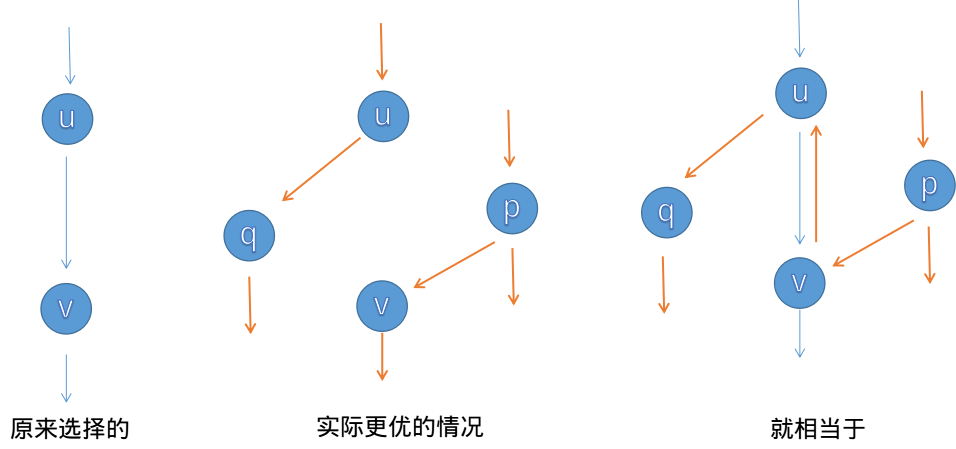
<h2>反向边的实现</h2>
因为你是一个指针选手,对于每个边都建一个指向其反向边的指针就可以了。
<h2>上述朴素算法太慢了</h2>
可以被一些奇妙的极限数据卡掉,大概就是有很大和很小的边权,如果增广策略不对,就会陷入增广许多次的情景,时间复杂度飞天。
例如下面这组数据: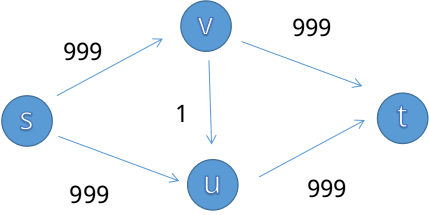
手动模拟一下就会发现它要循环许多遍!这是我们不可以接受的。
于是 Dinic 算法解决了这个问题。
<h2>Dinic 算法</h2>
Dinic 算法引入一个分层图的概念(不是分层图最短路),对于每一个节点记录一个 $level$ 表示到达源点的距离(边权看作 $1$ )。我们限制每次由 $u$ 增广出来的 $v$ 必须满足 $level_u + 1 = level_v$。这样就能防止上述的奇怪情况卡掉朴素算法。
Dinic 算法的时间复杂度理论上界是 $O(n^2m)$,但是绝大多数情况都跑不满。
<h2>当前弧优化</h2>
即每一次dfs增广时不从第一条边开始,而是记录点u之前循环到了哪一条边,以此来加速。
这样能快不少,更不容易跑到上界了
<h2>具体实现</h2>
<h3>结构体定义</h3>
我们定义点结构体(Node)和边结构体(Edge)
struct Node{
struct Edge firstEdge,curEdge; // curEdge 当前弧优化用
int level; // bfs 出来的层数
}node[MAXN];
struct Edge{
Node s,t;
Edge next,reverse; // reverse 记录这条边的反向边
int cap,flow; // cap 流量,flow 目前增广出来的经过这条边花费的最大流量
}pool[MAXM<<2],*frog = pool;
剩下的操作在代码里会给出注释。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 10000+5;
const int MAXM = 100000+5;
struct Node{
struct Edge firstEdge,curEdge;
int level;
}node[MAXN];
struct Edge{
Node s,t;
Edge next,reverse;
int cap,flow;
}pool[MAXM<<2],*frog = pool;
Edge New(Node s,Node *t,int cap){
Edge *ret = ++frog;
*ret = (Edge){s,t,s->firstEdge,NULL,cap,0};
return ret;
}
inline void add(int u,int v,int cap){
node[u].firstEdge = New(&node[u],&node[v],cap);
node[v].firstEdge = New(&node[v],&node[u],0);
node[u].firstEdge->reverse = node[v].firstEdge;
node[v].firstEdge->reverse = node[u].firstEdge;
// 建立边和反向边并且互相关联
}
int N,M,S,T;
inline bool bfs(Node s,Node t){
FOR(i,1,N){
node[i].level = 0;
node[i].curEdge = node[i].firstEdge; // 初始化 cur
}
std::queue<Node *> q;
q.push(s);s->level = 1;
while(!q.empty()){
Node *v = q.front();q.pop();
for(Edge *e = v->firstEdge;e;e = e->next){
if(e->flow < e->cap && !e->t->level){
e->t->level = v->level + 1;
if(e->t == t) return true;
q.push(e->t);
}
}
}
return false;
}
int dfs(Node s,Node t,int limit=INT_MAX){ // 寻找增广路
if(s == t) return limit;
for(Edge *&e = s->curEdge;e;e = e->next){ // 当前弧优化
if(e->flow < e->cap && e->t->level == s->level + 1){
int flow = dfs(e->t,t,std::min(limit,e->cap - e->flow));
if(flow > 0){ // 找到一条
e->flow += flow;
e->reverse->flow -= flow;
return flow;
}
}
}
return 0;
}
int dinic(){
int ans = 0;
while(bfs(&node[S],&node[T])){ // 一直到不能分层为止
int flow = dfs(&node[S],&node[T]);
while(flow > 0){ // 一直到不能增广位置
ans += flow;
flow = dfs(&node[S],&node[T]);
}
}
return ans;
}
int main(){
scanf("%d%d%d%d",&N,&M,&S,&T);
FOR(i,1,M){
int u,v,c;scanf("%d%d%d",&u,&v,&c);
add(u,v,c);
}
printf("%dn",dinic());
return 0;
}

One comment
太强了,wyh