<h1>定义</h1>

首先简要介绍一下 AC 自动机：Aho-Corasick automation，该算法在 1975 年产生于贝尔实验室，是著名的多模匹配算法之一。一个常见的例子就是给出 n 个单词，再给出一段包含m个字符的文章，让你找出有多少个单词在文章里出现过。要搞懂 AC 自动机，先得有模式树（字典树）Trie 和 KMP 模式匹配算法的基础知识。KMP 算法是单模式串的字符匹配算法，AC自动机是多模式串的字符匹配算法。
如果您还不会 KMP，点击这里
如果您还不会 Trie 树，点击这里
好了，默认您已经掌握了两种基础算法，正文开始。
首先如果一个模式串一个匹配串问模式串出现了几次？可以使用 $O(n+m)$ 的 KMP 算法来解决。但是有多个模式串怎么解决呢？显然直接跑很多次 KMP 是不切实际的，那么我们就要考虑用一种更加方便的方法来将这些模式串联系起来，于是我们就可以考虑将两者结合起来。

<h2>建立字典树</h2>

假设我们有这些单词：she,he,say,her,shr，我们可以构造一颗字典树：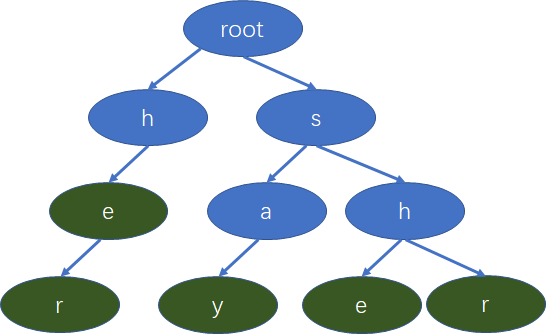

<h2>构造 fail 指针</h2>

这里是整个 AC 自动机的核心部分。
类似于 KMP 的 next 数组的思想，我们考虑在字典树上失配会怎么样：朴素的来说我们会返回到根重新来找，但是利用字典数上公共前缀的特性可以减少这些无用的计算量。

（图侵删）
那么考虑如何构造这个 fail 指针呢？
我们定义每个节点的 fail 指针的寻找方式为：沿着当前点的父亲的 fail 指针跳到一个点的儿子和这个节点代表的字母相同的点，则 fail 指针指向这个子节点。
形式化一下：设当前点是 $v$，则我们沿着 $fa_v$ 的 fail 指针一直跳到第一个点$t$ 满足 $t$ 的一个子节点和 $v$ 代表的字符相同，那么执行 v->fail = t->child

<h2>查找</h2>

查找就比较简单了吧 =-= 综合一下 KMP 和 Trie 树的查找即可。
按照这个字符串当前的数字在 Trie 树中搜索，一旦失配回溯到这个节点的 fail 指针指向的节点，并且继续往下找即可。

<h2>模板题 1</h2>

题目链接
题目描述：给定n个模式串和1个文本串，求有多少个模式串在文本串里出现过。
裸的 AC 自动机模板题，直接套板子就可以了。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 3000000+5;
const int MAXM = 26;

struct Node{
    int sum;
    Node next[26],fail;
}pool[MAXN],frog = pool,root;

Node *New(){
    Node *ret = ++frog;
    ret->sum = 0;ret->fail = NULL;
    FOR(i,0,25) ret->next[i] = NULL;
    return ret;
}

void build(){
    std::queue<Node *> q;
    FOR(i,0,25){
        if(root->next[i]){
            root->next[i]->fail = root;
            q.push(root->next[i]);
        }
    }
    while(!q.empty()){
        Node *v = q.front();q.pop();
        FOR(i,0,25){
            if(v->next[i]){
                Node *t = v->fail;
                while(t){
                    if(t->next[i]){
                        v->next[i]->fail = t->next[i];
                        break;
                    }
                    t = t->fail;
                }
                if(!t) v->next[i]->fail = root;
                q.push(v->next[i]);
            }
        }
    }
}

void insert(char *str){
    Node *v = root;int len = strlen(str+1);
    FOR(i,1,len){
        int x = str[i] - 'a';
        if(!v->next[x]) v->next[x] = New();
        v = v->next[x];
    }
    v->sum++;
}

int query(char *str){
    int len = strlen(str+1),ans=0;
    Node *v = root;
    FOR(i,1,len){
        int x = str[i] - 'a';
        while(!v->next[x] && v != root) v = v->fail;
        v = v->next[x];
        if(!v) v = root;
        Node *t = v;
        while(t != root){
            if(t->sum >= 0){
                ans += t->sum;
                t->sum = -1;
            }
            else break;
            t = t->fail;
        }
    }
    return ans;
}

int N;
char str[MAXN];

int main(){
    root = New();scanf("%d",&N);
    FOR(i,1,N){
        scanf("%s",str+1);
        insert(str);
    }
    build();
    scanf("%s",str+1);
    printf("%dn",query(str));
    return 0;
}

<h2>模板题 2</h2>

题目链接
题目描述：有 $N$ 个由小写字母组成的模式串以及一个文本串 $T$。每个模式串可能会在文本串中出现多次。你需要找出哪些模式串在文本串 $T$ 中出现的次数最多。
这个题目实质上差不多，就是我们对于 Trie 树上的每一个单词终点记录的不再是一个计数器，而是对应单词的编号，遇到编号累加答案最后排个序输出就可以了。

#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const int MAXN = 100000+5;
const int MAXM = 26;

struct Node{
    int val;
    Node next[MAXM],fail;
}pool[MAXN],frog = pool,root;

Node *New(){
    Node *ret = ++frog;
    ret->val = 0;ret->fail = NULL;
    FOR(i,0,25) ret->next[i] = NULL;
    return ret;
}

void insert(char *str,int val){
    int len = strlen(str+1);
    Node *v = root;
    FOR(i,1,len){
        int x = str[i] - 'a';
        if(!v->next[x]) v->next[x] = New();
        v = v->next[x];
    }
    v->val = val;
}

void build(){
    std::queue<Node *> q;
    FOR(i,0,25){
        if(root->next[i]){
            q.push(root->next[i]);
            root->next[i]->fail = root;
        }
    }
    while(!q.empty()){
        Node *v = q.front();q.pop();
        FOR(i,0,25){
            if(v->next[i]){
                Node *t = v->fail;
                while(t){
                    if(t->next[i]){
                        v->next[i]->fail = t->next[i];
                        break;
                    }
                    t = t->fail;
                }
                if(!t) v->next[i]->fail = root;
                q.push(v->next[i]);
            }
        }
    }
}

std::pair<int,int> ans[MAXN];

void query(char *str){
    int len = strlen(str+1);
    Node *v = root;
    FOR(i,1,len){
        int x = str[i] - 'a';
        while(!v->next[x] && v != root) v = v->fail;
        v = v->next[x];
        if(!v) v = root;
        Node *t = v;
        while(t != root){
            // if(t->val > 0) ans[t->val].first++;
            // else break;
            ans[t->val].first++;
            t = t->fail;
        }
    }
}

int N;
char str2000;
char q[1000000+5];

bool cmp(const std::pair<int,int> &a,const std::pair<int,int> &b){
    return a.first == b.first ? a.second < b.second : a.first > b.first;
}

inline void init(){
    CLR(pool,0);frog = pool;
    root = New();CLR(ans,0);
    //CLR(q,0);CLR(str,0);
}
int cnt=0;
int main(){
    //freopen("testdata.in","r",stdin);
    //freopen("testdata.out","w",stdout);
    while(19260817){
        scanf("%d",&N);if(!N) break;
        init();
        FOR(i,1,N){
            scanf("%s",str[i]+1);
            ans[i] = std::make_pair(0,i);
            insert(str[i],i);
        }
        build();
        scanf("%s",q+1);
        query(q);
        std::sort(ans+1,ans+N+1,cmp);
        printf("%dn",ans[1].first);
        printf("%sn",str[ans[1].second]+1);
        FOR(i,2,N){
            if(ans[i].first == ans[i-1].first){
                printf("%sn",str[ans[i].second]+1);
            }
            else break;
        }
    }
    return 0;
}

<h1>总结</h1>

AC 自动机是一种简单的自动机，可以和 dp 等算法巧妙结合。我听说有人把莫比乌斯反演放在了这上面。
但是注意千万不要把这种数据结构和某些评测软件的自动"AC"机混为一谈，当然我很仁慈的不给出自动"AC"机的代码以供大家警示大家不要用错名词$qwq$。