<h1>定义</h1>
<h2>链剖分</h2>
首先我们知道,OI 中能见到的有重链剖分,实链剖分和长链剖分。
重链剖分已经在之前的树链剖分中熟练运用过了,长链剖分不常考,所以这次我们先来看一看实链剖分。
实链剖分:将某一个儿子的连边划分为实边,而连向其他子树的边划分为虚边。
我们发现边的虚实是可以动态变化的,因此可以使用更高级、更灵活的 Splay 来维护每一条由若干实边连接而成的实链,基于这个原理,LCT 才能解决很多的动态树问题。
- 查询,修改链信息
- 随意换根
- 动态连边,删边
- 合并树,分离树
- 动态维护连通性
Link-Cut-Tree(简称 LCT) 的性质如下:
- 每一个 Splay 维护的是一条从上到下按在原树中深度严格递增的路径,且中序遍历 Splay 得到的每个点的深度序列严格递增
- 每个节点包含且仅包含在一个 Splay 中
- 实边是包含在 Splay 中的,而虚边是节点连向另一个 Splay 的边。
<h1>操作</h1>
<h2>Access 操作</h2>
这是 LCT 的核心操作,其他的操作都是基于此完成的。
这个操作就是在满足 LCT 性质的前提下,将任意一个节点和根节点之间的路径变成一条实链。
下面的图参考YangZhe的论文:
一开始我们有一个这样的树(虚线表示虚边)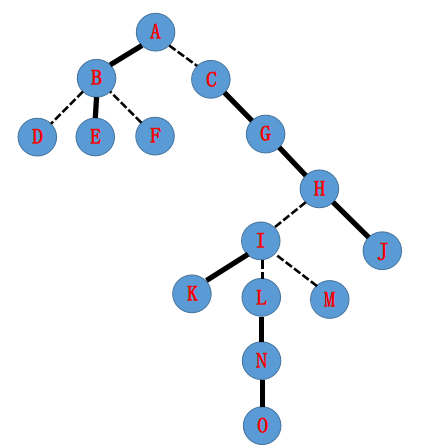
那么 LCT 有可能如下图所示(每个框里的元素都在一个 Splay 中)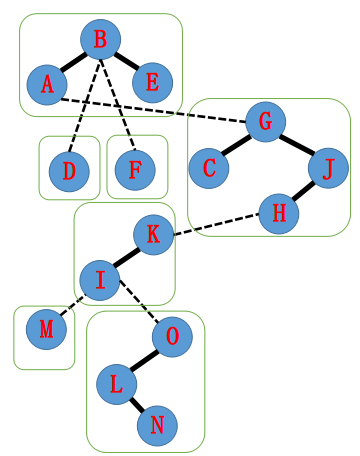
现在我们要执行 access(N) 操作了。
由性质 2 可得为了使得 A 到 N 上全是实边,需要使得其他的边变成虚边。
所以可能划分成这样: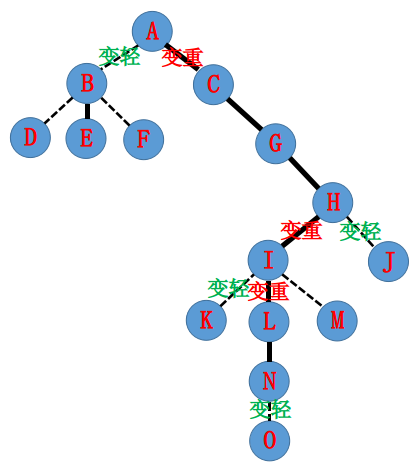
怎么实现这一个过程呢?我们可以让 N 点一直跳 Splay 来实现。
首先执行 Splay(N) 将 N 伸展为根节点,为了满足性质二,$N-O$ 要变为轻边。
为了满足性质一:单方面将 N 的右儿子设置为空。
然后变成下图: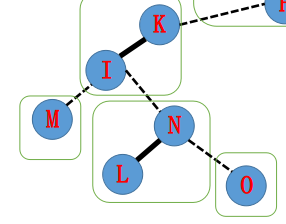
我们接着把 N 指向的点 I 也伸展到它所属的 Splay 的根节点,为了维护性质,I 到 K 的边要单方面废除,这时候 I 到 L 可以变成实边了,按照性质 1 将 N 放在 I 的右儿子上。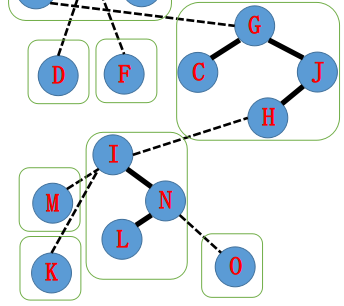
多次重复该过程直到路径上全为实边。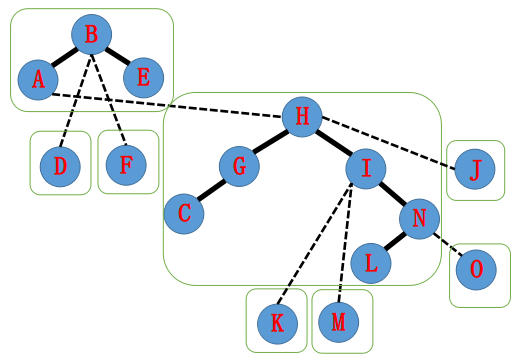
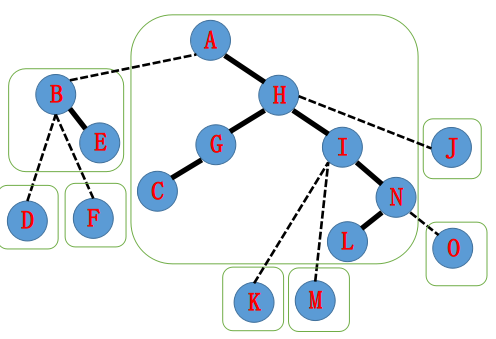
归纳一下上述过程:
- 伸展到当前 Splay 的根节点
- 交换儿子
- 更新信息(pushup)
- 操作点换为轻边指向的父亲,转1
inline void access(int x){
for(int y=0;x;x = f[y = x]){
splay(x);rc = y;pushup(x);
}
}
<h2>makeroot 操作</h2>
钦定新根操作。我们在运用中有可能查询两点路径无论如何不可能在一个 Splay 中,这个时候我们考虑改变树的根而保持树维护信息不变,将其放在一个 Splay 里求解。
首先一定要让 $x$ 和 $root$ 在一个 Splay 里,然后将 $x$ 伸展到根。然后注意到一开始 $x$ 的深度是最大的,那么我们如果翻转整个 Splay,$x$ 就变成了深度最小的节点(即根),所以我们打个标记翻转即可。
inline void reverse(int x){
std::swap(lc,rc);tag[x] ^= 1;
}
inline void makeroot(int x){
access(x);splay(x);reverse(x);
}
<h2>findroot 操作</h2>
查询根节点操作,主要用来判断连通性。
大概就是先让 $x$ 成为 Splay 中的根,然后按照定义一一直走左儿子,最后的那个点一定是深度最小的(即根)。
inline int findroot(int x){
access(x);splay(x);
while(lc) pushdown(x),x=lc;
// splay(v); 某势能分析指出这一句话是要加来保证复杂度的,但是不加貌似没错.....
return x;
}
<h2>split 操作</h2>
我们想将 $x$ 到 $y$ 的路径放入一个 Splay 里,需要借助 makeroot 操作进行实现。
直接将 $x$ 钦定为根,然后将 $y$ 放入和 $x$ 一样的 Splay 里并伸展为 Splay 的根节点,这样我们查询路径信息其实就是查询 $y$ 的信息了 qwq。
inline void split(int x,int y){
makeroot(x);access(y);splay(y);
}
<h2>link 操作</h2>
连边操作。特判如果这条边不存在直接加一条虚边。
inline void link(int x,int y){
makeroot(x);
if(findroot(y) != x) f[x] = y;
}
<h2>cut 操作</h2>
删除一条边。注意到这里特判比较多,即特判以下情况:
- 不存在这条边
- $x$ 的父亲不是 $y$,即 $x$ 和 $y$ 虽然在一个 Splay 中但是没有连边。
- $x$ 的右子树非空,这时以 $y$ 为根开始的中序遍历中 $x$ 和 $y$ 不在一起,即没有边。
inline void cut(int x,int y){
makeroot(x);
if(findroot(y) == x && f[x] == y && !rc){
f[x] = childy = 0;
pushup(y);
}
}
此外还要注意 LCT 中的 Splay 和日常写的有些不一样,有些地方是要判断的。
注意 findroot 判断连通性很慢,如果题目只有合并操作的话,建议使用并查集。
<h1>完整代码</h1>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define lc childx
#define rc childx
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 300000+5;
int f[MAXN],childMAXN,val[MAXN],s[MAXN],tag[MAXN];
bool r[MAXN];
inline bool nroot(int x){
return child[f[x]][0] == x || child[f[x]][1] == x;
}
inline void pushup(int x){
s[x] = s[lc]^s[rc]^val[x];
}
inline void reverse(int x){
int t = lc;lc = rc;rc = t;tag[x] ^= 1;
}
inline void pushdown(int x){
if(tag[x]){
if(lc) reverse(lc);
if(rc) reverse(rc);
tag[x] = 0;
}
}
inline void rotate(int x){
int y = f[x],z = f[y];int k = childy==x,w = childx;
if(nroot(y)) childz[1]==y] = x;
childx = y;childy = w;
if(w) f[w] = y;
f[y] = x,f[x] = z;
pushup(y);
}
int st[MAXN];
inline void splay(int x){
int y = x,z;st[z = 1] = y;
// std::stack<int> S;
// S.push(y);
while(nroot(y)) st[++z] = y = f[y];//S.push(y=f[y]);
while(z) pushdown(st[z--]);
//while(!S.empty()) pushdown(S.top()),S.pop();
while(nroot(x)){
y = f[x];z = f[y];
if(nroot(y)) rotate((childy == x) ^ (childz == y) ? x : y);
rotate(x);
}
pushup(x);
}
inline void access(int x){
for(int y = 0;x;x = f[y = x]){
splay(x);rc = y;pushup(x);
}
}
inline void makeroot(int x){
access(x);splay(x);reverse(x);
}
inline int findroot(int x){
access(x);splay(x);
while(lc) pushdown(x),x = lc;
// splay(v); 某势能分析指出这一句话是要加来保证复杂度的,但是不加貌似没错.....
return x;
}
inline void split(int x,int y){
makeroot(x);access(y);splay(y);
}
inline void link(int x,int y){
makeroot(x);
if(findroot(y) != x) f[x] = y;
}
inline void cut(int x,int y){
makeroot(x);
if(findroot(y) == x && f[x] == y && !rc){
f[x] = childy = 0;
pushup(y);
}
}
int N,M;
int main(){
scanf("%d%d",&N,&M);
FOR(i,1,N) scanf("%d",val+i);
FOR(i,1,M){
int opt,x,y;scanf("%d%d%d",&opt,&x,&y);
if(opt == 0) split(x,y),printf("%dn",s[y]);
if(opt == 1) link(x,y);
if(opt == 2) cut(x,y);
if(opt == 3) splay(x),val[x] = y;
}
return 0;
}

2 comments
Orz
Orz