记录一下本人目前会做的 GSS 系列题目。
目前已经完成 GSS1,GSS3,GSS4,GSS5。
<h2>GSS1</h2>
<h3>题目描述</h3>
求最大子段和,序列的值可能为负数。
其中长度 $\leq 50000$。
<h3>解题报告</h3>
线段树维护这个序列。
线段树中维护四个值:$sum,lans,rans,ans$,分别表示当前序列的和,前缀最大值,后缀最大值,和最大子段和。
合并的时候暴力维护一下就可以了。
时间复杂度 $O(nlog_2n)$。
<h3>代码</h3>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
namespace fastIO{
#define BUF_SIZE 100000
#define OUT_SIZE 100000
#define ll long long
bool IOerror=0;
inline char nc(){
static char buf[BUF_SIZE],p1=buf+BUF_SIZE,pend=buf+BUF_SIZE;
if (p1==pend){
p1=buf; pend=buf+fread(buf,1,BUF_SIZE,stdin);
if (pend==p1){IOerror=1;return -1;}
}
return *p1++;
}
inline bool blank(char ch){return ch==' '||ch=='n'||ch=='r'||ch=='t';}
inline void read(int &x){
bool sign=0; char ch=nc(); x=0;
for (;blank(ch);ch=nc());
if (IOerror)return;
if (ch=='-')sign=1,ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
if (sign)x=-x;
}
inline void read(ll &x){
bool sign=0; char ch=nc(); x=0;
for (;blank(ch);ch=nc());
if (IOerror)return;
if (ch=='-')sign=1,ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
if (sign)x=-x;
}
#undef ll
#undef OUT_SIZE
#undef BUF_SIZE
};
using namespace fastIO;
const int MAXN = 50000 + 5;
struct Node New(int ,int ,Node ,Node *);
struct Node{
int l,r;LL lmax,rmax,ans,sum;
Node lc,rc;
inline void init(){
l = r = sum = 0;
lmax = rmax = ans = LLONG_MIN;
lc = rc = NULL;
}
static Node *build(int l,int r){
int mid = (l + r) >> 1;
return (l == r) ? New(l,r,NULL,NULL) : New(l,r,build(l,mid),build(mid+1,r));
}
inline void pushup(){
lmax = std::max(lc->lmax,lc->sum+rc->lmax);
rmax = std::max(rc->rmax,rc->sum+lc->rmax);
sum = lc->sum + rc->sum;
ans = std::max(std::max(lc->ans,rc->ans),lc->rmax+rc->lmax);
}
inline void update(int x,int pos){
if(l == r){
lmax = rmax = sum = ans = x;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid) lc->update(x,pos);
else rc->update(x,pos);
pushup();
}
inline Node query(int L,int R){
if(L == l && R == r){
return (Node){0,0,lmax,rmax,ans,sum,NULL,NULL};
}
int mid = (l + r) >> 1;
if(R <= mid) return lc->query(L,R);
if(L > mid) return rc->query(L,R);
Node la = lc->query(L,mid),ra = rc->query(mid+1,R),ret;
ret.lmax = std::max(la.lmax,la.sum+ra.lmax);
ret.rmax = std::max(ra.rmax,ra.sum+la.rmax);
ret.sum = la.sum + ra.sum;
ret.ans = std::max(std::max(la.ans,ra.ans),la.rmax+ra.lmax);
return ret;
}
}pool[(MAXN<<1)+1],frog = pool,segt;
Node New(int l,int r,Node lc,Node *rc){
Node *ret = ++frog;
ret->l = l;ret->r = r;
ret->lmax = ret->rmax = ret->ans = LLONG_MIN;
ret->sum = 0;
ret->lc = lc;ret->rc = rc;
return ret;
}
int N,M;
int main(){
read(N);
segt = Node::build(1,N);
FOR(i,1,N){
int x;read(x);
segt->update(x,i);
}
read(M);
while(M--){
int x,y;read(x);read(y);
printf("%lldn",segt->query(x,y).ans);
}
return 0;
}
<h2>GSS3</h2>
一点都没变......中间直接加上单点修改的操作就行了。
可以去我之前写的博客里观看,写的比较详细。
<h2>GSS4</h2>
<h3>题目描述</h3>
维护一个序列,支持下列操作:
- 区间开方(向下取整)
- 区间和
其中区间长度 $\leq 10^5$,所有元素的和 $\leq 10^{18}$。
<h3>解题报告</h3>
发现数一直开方最后会变成 $0$ 或 $1$ 。我们直接维护区间最大值就可以,当最大值 $\leq 1$ 的时候就不需要修改,否则暴力递归下去即可。因为数不是很大,$10^9$ 范围的数开方 $9$ 次就不用开方了,复杂度得以保证。
<h3>代码</h3>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 200000 + 5;
struct Node New(int ,int ,Node ,Node *);
struct Node{
int l,r;
LL sum,max;
Node lc,rc;
static Node *build(int l,int r){
int mid = (l + r) >> 1;
return (l == r) ? New(l,r,NULL,NULL) : New(l,r,build(l,mid),build(mid+1,r));
}
inline void pushup(){
sum = lc->sum + rc->sum;
max = std::max(lc->max,rc->max);
}
inline void update(LL x,int pos){
if(l == r){
max = sum = x;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid) lc->update(x,pos);
else rc->update(x,pos);
pushup();
}
inline void modify(int L,int R){
if(max <= 1) return;
if(l == r){
max = sum = std::sqrt(sum);
return;
}
int mid = (l + r) >> 1;
if(R <= mid) lc->modify(L,R);
else if(L > mid) rc->modify(L,R);
else lc->modify(L,mid),rc->modify(mid+1,R);
pushup();
}
inline LL query(int L,int R){
if(l == L && r == R) return sum;
int mid = (l + r) >> 1;
if(R <= mid) return lc->query(L,R);
if(L > mid) return rc->query(L,R);
return lc->query(L,mid)+rc->query(mid+1,R);
}
}pool[MAXN<<2],frog = pool,segt;
Node New(int l,int r,Node lc,Node *rc){
Node *ret = ++frog;
ret->l = l;ret->r = r;
ret->lc = lc;ret->rc = rc;
ret->sum = 0ll;ret->max = LLONG_MIN;
return ret;
}
int N,M,ts;
inline void Solve(){
printf("Case #%d:n",++ts);
frog = pool;segt = NULL;
CLR(pool,0);
segt = Node::build(1,N);
FOR(i,1,N){
LL x;scanf("%lld",&x);
segt->update(x,i);
}
scanf("%d",&M);
while(M--){
int opt,x,y;
scanf("%d%d%d",&opt,&x,&y);
if(x > y) std::swap(x,y);
if(opt){
printf("%lldn",segt->query(x,y));
}
else{
segt->modify(x,y);
}
}
puts("");
}
int main(){
while(~scanf("%d",&N)) Solve();
return 0;
}
<h2>GSS5</h2>
<h3>题目描述</h3>
$GSS1$的升级版。这次限定左端点在 $[x_1,y_1]$ 之间,右端点在 $[x_2,y_2]$ 之间。
<h3>解题报告</h3>
只需要分类讨论一下就可以了qwq
如果 $y_1 \leq x_2$ 即两段区间没有交点,那么一定是 $[x_1,y_1]$ 的后缀最大值加上 $[y_1,x_2]$ 的和(必须经过)加上 $[x_2,y_2]$ 的前缀最大值。
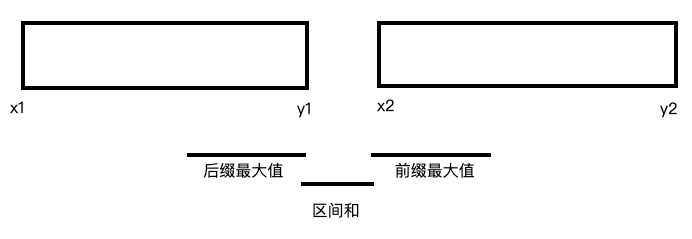
如果有交点 ($y_1 > x_2$),那么就要进行一波分类讨论:
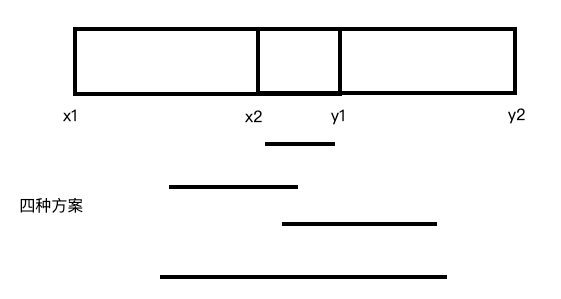
第一条线段:当 $x_2 \leq x,y \leq y_1$ 的时候,只需要求出 $[x_2,y_1]$ 的最大子段和。
第二条线段:当 $x_1 \leq x < x_2,x_2 \leq y \leq y_1$ 的时候,答案是 $[x_1,x_2)$ 的最大后缀和 $+$ $[x_2,y_1] $ 的最大前缀和。
第三条线段:当 $x_2 \leq x \leq y_1,y_1 < y \leq y_2$ 的时候,答案是$[x_2,y_1]$ 的最大后缀和 $+$ $(y_1,y_2]$ 的最大前缀和。
第四条线段:当 $x_1 \leq x < x_2,y_1 < y \leq y_2$ 的时候,答案是 $[x_1,x_2)$ 的最大后缀和 $+$ $[x_2,y_1]$ 的区间和 $+$ $(y_1,y_2]$ 的最大前缀和。
注意特判一下不是必选的区间和 $0$ 比较就可以了,还有一定要在查询的时候判断区间不可行退出,还要注意区间临界点处理的细节。
还有不要定义 $y1,y2$ 这种变量,会和 $cmath$ 库冲突的。
总体来说还是很水的,代码细节比较多
<h3>代码</h3>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define Re register
#define LL long long
#define U unsigned
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define CLR(i,a) memset(i,a,sizeof(i))
#define BR printf("--------------------n")
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
namespace fastIO{
#define BUF_SIZE 100000
#define OUT_SIZE 100000
#define ll long long
bool IOerror=0;
inline char nc(){
static char buf[BUF_SIZE],p1=buf+BUF_SIZE,pend=buf+BUF_SIZE;
if (p1==pend){
p1=buf; pend=buf+fread(buf,1,BUF_SIZE,stdin);
if (pend==p1){IOerror=1;return -1;}
}
return *p1++;
}
inline bool blank(char ch){return ch==' '||ch=='n'||ch=='r'||ch=='t';}
inline void read(int &x){
bool sign=0; char ch=nc(); x=0;
for (;blank(ch);ch=nc());
if (IOerror)return;
if (ch=='-')sign=1,ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
if (sign)x=-x;
}
inline void read(ll &x){
bool sign=0; char ch=nc(); x=0;
for (;blank(ch);ch=nc());
if (IOerror)return;
if (ch=='-')sign=1,ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
if (sign)x=-x;
}
#undef ll
#undef OUT_SIZE
#undef BUF_SIZE
};
//using namespace fastIO;
#define read(x) std::cin >> x
const int MAXN = 20000 + 5;
#define int long long
struct Node New(int ,int ,Node ,Node *);
struct Node{
int l,r;LL lmax,rmax,ans,sum;
Node lc,rc;
inline void init(){
l = r = sum = 0;
lmax = rmax = ans = LLONG_MIN;
lc = rc = NULL;
}
static Node *build(int l,int r){
int mid = (l + r) >> 1;
return (l == r) ? New(l,r,NULL,NULL) : New(l,r,build(l,mid),build(mid+1,r));
}
inline void pushup(){
lmax = std::max(lc->lmax,lc->sum+rc->lmax);
rmax = std::max(rc->rmax,rc->sum+lc->rmax);
sum = lc->sum + rc->sum;
ans = std::max(std::max(lc->ans,rc->ans),lc->rmax+rc->lmax);
}
inline void update(int x,int pos){
if(l == r){
lmax = rmax = sum = ans = x;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid) lc->update(x,pos);
else rc->update(x,pos);
pushup();
}
inline Node query(int L,int R){
if(L>R) return (Node){0,0,0,0,0,0,NULL,NULL};
if(L == l && R == r){
return (Node){0,0,lmax,rmax,ans,sum,NULL,NULL};
}
int mid = (l + r) >> 1;
if(R <= mid) return lc->query(L,R);
if(L > mid) return rc->query(L,R);
Node la = lc->query(L,mid),ra = rc->query(mid+1,R),ret;
ret.lmax = std::max(la.lmax,la.sum+ra.lmax);
ret.rmax = std::max(ra.rmax,ra.sum+la.rmax);
ret.sum = la.sum + ra.sum;
ret.ans = std::max(std::max(la.ans,ra.ans),la.rmax+ra.lmax);
return ret;
}
}pool[(MAXN<<2)+1],frog = pool,segt;
Node New(int l,int r,Node lc,Node *rc){
Node *ret = ++frog;
ret->l = l;ret->r = r;
ret->lmax = ret->rmax = ret->ans = LLONG_MIN;
ret->sum = 0;
ret->lc = lc;ret->rc = rc;
return ret;
}
int N,M;
inline void Solve(){
read(N);
frog = pool;CLR(pool,0);
segt = Node::build(1,N);
FOR(i,1,N){
int x;read(x);
segt->update(x,i);
}
int x1,y_1,x2,y_2;
read(M);LL ans;
while(M--){
read(x1);read(y_1);read(x2);read(y_2);
if(y_1 < x2)
ans = std::max(segt->query(x1,y_1-1).rmax,0ll) + segt->query(y_1,x2).sum + std::max(segt->query(x2+1,y_2).lmax,0ll);
else{
ans = segt->query(x2,y_1).ans;
ans = std::max(ans,segt->query(x2,y_1).lmax + segt->query(x1,x2-1).rmax);
ans = std::max(ans,segt->query(y_1+1,y_2).lmax + segt->query(x2,y_1).rmax);
ans = std::max(ans,segt->query(x2,y_1).sum + std::max(segt->query(x1,x2-1).rmax,0ll) + std::max(segt->query(y_1+1,y_2).lmax,0ll));
}
printf("%lldn",ans);
}
}
signed main(){
int T;read(T);
while(T--) Solve();
return 0;
}
