<h2>题目描述</h2>

We have a convex polygon in the XY plane. The vertices of the polygon are the points (x[0], y[0]), (x[1], y[1]), ... in clockwise order. You are given the vector <int>s x and y.

In order to make the implementation simpler the polygon and its representation satisfy some additional constraints. Please read the Constraints section carefully.

A three-dimensional solid is obtained by rotating this polygon around the Y axis. Compute and return the volume of the resulting solid.

<h2>题目大意</h2>

你得到了一个二维凸包，这个凸包满足以下奇怪性质:

1. 在 y 轴上恰好有两个点
2. 设在 y 轴上的两个点分别是 $(0,y_{min})$ 与 $(0,y_{max})$，其中 $y_max > y_min$，那么其 他所有点的 $y$ 坐标都介于 $[y_{min},y_{max}]$ 之间
3. 没有重点，没有三点共线
   你需要输出将这个凸包绕 $y$ 轴旋转得到的立体图形的体积。

绝对误差或相对误差小于 $10^{-9}$ 即为正确。

<h2>解题报告</h2>

又一道计算几何题。。。。。
首先要知道有一个神奇的东西，用来算函数图像绕某定轴旋转后的立体面积的：Disc Intergration
(为了不用科学上网，我把和这题有关的内容搬过来)：
“If the function to be revolved is a function of x, the following integral represents the volume of the solid of revolution:
$$\pi \int_{a}^{b} R(x)^2 dx$$
where $R(x)$ is the distance between the function and the axis of rotation. This works only if the axis of rotation is horizontal (example: $y = 3$ or some other constant).”
我们考虑按照 y 轴切成很多片，对每一片分别算完答案后再拼起来。
每一小片可以近似的看成一个去掉头的圆锥或者是圆柱，我们找到与当前切割线 $y=y0$ 相交的绝对值最大的那一条，然后累加它的体积。如果切得足够多精度误差就会小于 $10^{-9}$ 了吧。
核心思想就是这样。。。然后我们放一下代码并解释一些东西。

#line 5 "problem.cpp"
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <cmath>
#include <ctime>
#include <queue>
#include <stack>
#include <map>
#include <set>

#define fi first
#define se second
#define U unsigned
#define P std::pair<double,double>
#define Re register
#define LL long long
#define pb push_back
#define MP std::make_pair
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl

const double EPS = 1e-9;
const double pi = acos(-1);

class PolygonRotation{
public:

    inline double ds(P p1,P p2,double y){
        if(p1.se == p2.se) return abs(std::max(p1.fi,p2.fi));
        return std::abs(p1.fi+1.0(p2.fi-p1.fi)/(p2.se-p1.se)(y-p1.se));
    }

    int n;
    
    double f(double y,const std::vector<int> &X,const std::vector<int> &Y){
        double max = 0.0;
        FOR(i,0,n-1){
            if(std::abs(Y[i]-y) <= EPS) max = std::max(max,1.0*X[i]);
            int nxt = i < n-1 ? i+1 : 0;
            if(std::min(Y[i],Y[nxt]) > y) continue;
            if(std::max(Y[i],Y[nxt]) < y) continue;
            double t = ds(MP(X[i],Y[i]),MP(X[nxt],Y[nxt]),y);
            max = std::max(max,t);
        }
        //DEBUG(max);
        return pimaxmax;
    }

    double getVolume(std::vector <int> X, std::vector <int> Y){
        double a = std::min_element(all(Y)),b = std::max_element(all(Y));
        n = X.size();
        const int N = 1e6;
        double sum = 0.0;
        double h = (b-a)/N;
        FOR(i,0,N){
            double y = a+h*i;
            sum += f(y,X,Y) * (((i == 0) || (i == N)) ? 1 : ((i&1) ? 4 : 2));
        }
        sum *= h;sum /= 3.0;
        return sum;
    }
};

<h2>一些 Simple 的问题</h2>

统计答案时的代码相信有些人看不懂，所以我略微解释一下：
为什么奇数位乘 4，而偶数位乘 2 呢？首先那个积分我们是不能直接算的（我们也不会算），于是我们可以将它近似展开：

$$ \int_{a}^b f(x)dx = \sum_{i = 2}^n \frac{\Delta x}{3}(y_{n-2}+4y_{n-1}+y_n) $$

推导大概如下：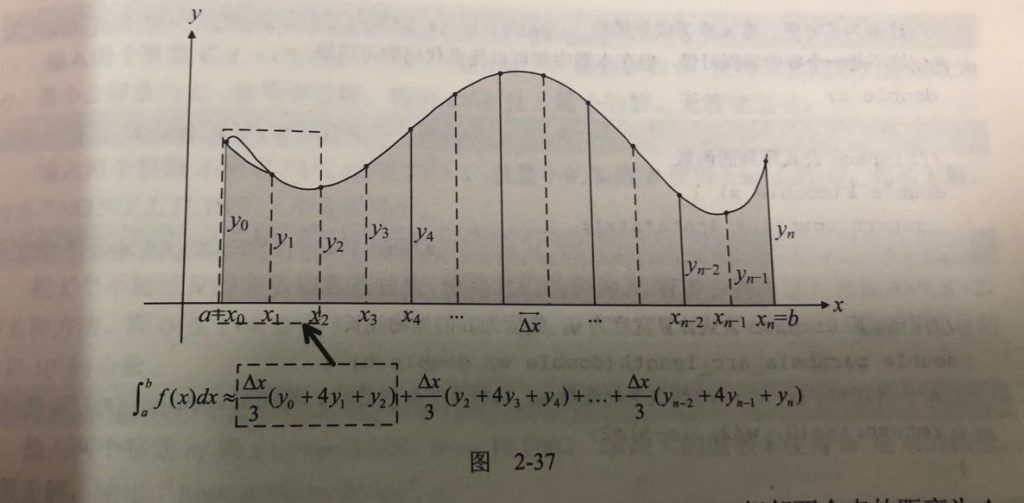

然后写一下每一个 y 对答案的贡献，就得到了最开始和最后贡献是 1 倍，其余奇数位 4 倍偶数位 2 倍了。