排版彻底崩了不管了 QAQ
基础概念
随机变量:有多种可能的取值的变量。
$P(A)$:事件 $A$ 发生的概率。
$E(X)$:随机变量 X 的期望值,$E(X) = \sum_{x} P(x=i)*i$
独立事件:互相不影响的事件,满足 $P(AB) = P(A)P(B),E(AB) = E(A)E(B)$
常用公式
$$\sum_{i=0}^n x^i = \frac{1-x^{n+1}}{1-x}$$
$$\sum_{i=0}^{\infty}\frac{1}{1-x},x \in (0,1)$$
期望的线性性:$\forall X,Y ,E[X+Y] = E[X]+E[Y]$
对于离散变量 $X$,$P(X=K) = P(X \leq K)-P(X \leq K-1)$
概率为 $p$ 的事件期望 $\frac{1}{p}$ 次发生,推导:
$$ \begin{align*} E(X) &= \sum_{i} P(X=i)i \\ &= \sum_{i} (P(x \geq i)-P(x \geq i+1))i \\ &= \sum_{i} ((1-p)^{i-1}-(1-p)^i)i \\ &= \sum_{i} (1-p)^i \\ &= \frac{1}{p} \end{align*} $$
小问题
拿球问题
箱子里有 $n$ 个球 $1 \cdots n$,你要从里面拿 $m$ 次球,求取出的数字之和的期望。
- 取出后放回
每一次取出的期望是 $\frac{n(n+1)}{2n} = \frac{n+1}{2}$,根据期望的线性性,得到取出 $m$ 次的期望是 $\frac{m(n+1)}{2}$
- 取出后不放回
首先设每次的结果 $S = \sum_{i=1}^n x_i * i$,其中 $x_i = [\text{取出了 $i$}]$。根据期望的线性性,我们得到
$$E[S] = \sum_{i=1}^n E[x_i]*i$$
考虑 $x$ 的取值是 $0,1$,所以 $E[x_i] = P[x_i]$。
发现 $P[x_i] = \frac{(^{n-1}_{m-1})}{(^n_m)} = \frac{m}{n}$,所以 $E[S] = \frac{m}{n} * \frac{n(n+1)}{2} = \frac{m(n+1)}{2}$
- 取出后有 $p_1$ 的几率放回,有 $p_2$ 的几率放回两个。
设$S=\sum_{i=1}%n x_i *i$,其中 $x_i$ 是出现次数。
所以只需要求 $E(x)$。发现一定均匀考虑了所有情况,所以 $\forall i,j ,E(i) = E(j)$。
根据期望的线性性有 $\sum_{i=1}^n E(i) = m$,所以 $E(i) = \frac{m}{n}$,也就有 $E(S) = \frac{m(n+1)}{2}$
上述三种情况的期望步数都一样,本质原因是过程中所有的球都是等价的(虽然我现在还是不会发现某些题目中的等价性质 Orz)。
游走问题
在⼀条 $n$ 个点的链上游⾛,求从⼀端⾛到另一端的期望
设 $f_i$ 表示 $i$ 第一次游走到 $i+1$ 的期望步数,显然 $f_1 = 1$。
考虑在 $i$ 点的可行策略可以得到转移 $f_{i} = \frac{1}{2}* 1 + \frac{1}{2}(1+f_{i-1}+f_{i})$,略加整理可得 $f_{i} = 2+f_{i-1}$,有 $f_n = (n-1)^2$.
- 在⼀张 $n$ 个点的完全图上游走,求从⼀个点走到另⼀个点的期望
显然从任意一个点到任意一个点的期望步数是相同的,概率也是相同的。考虑每次到达指定点是一个概率为 $\frac{1}{n-1}$ 的事件,期望就是 $n-1$。
- 在⼀张 $2n$ 个点的完全二分图上游走,求从一个点⾛到另⼀个点的期望
类似于完全图,这里每一边的点概率均等。我们设 $E_1,E_2$ 分别表示从同侧点到达目标点的代价和异侧点到目标点的代价。转移有 $E_1 = \frac{1}{2} + \frac{1}{2}(1+E_2)$,$E_2 = 1+E_1$。
可以得到 $E_2 = 2n-1$,$E_1 = 2n$。
- 在⼀张 $n$ 个点的菊花图上游走,求从⼀个点走到另⼀个点的期望
菊花图上每个非根点到非根点,根点到非根点,非根点到根点的期望都是相同的。
并且考虑 非根点之间并没有任何不同 但是在根点和非根点之间是区分出题目给出的起点和终点的。
所以设 $E_1$ 表示根点到非根点的期望, $E_2$ 表示非根点到非根点的期望。(显然非根点到根点的期望为 $1$)。所以可以得到 $E_1 = \frac{1}{n-1}+\frac{n-2}{n-1}(1+E_2)$,$E_2 = 1+E_1$。
可以得到 $E_1 = 2n-3,E_2 = 2n-2$。
- 在⼀棵 $n$ 个点的树上游走,求从根走到 $x$ 的期望步数
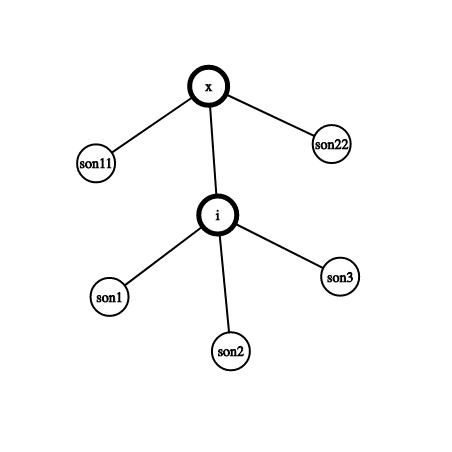
考虑树形 dp。设 $x$ 为 $i$ 的父亲,$d[v]$ 表示点 $v$ 的度数
,$son[v]$ 表示 $v$ 的孩子集合。
设 $f_i$ 表示 $i$ 走到它父亲的期望步数,$g_i$ 表示 $i$ 的父亲走到 $i$ 的期望步数。
可以写出 $f$ 的转移:
$$f_{i} = \frac{1+(\sum_{v \in son[i]}1+f_v+f_i)}{d_i}$$
化简可得:
$$f_{i} = d[i]+\sum_{v \in son_i} f_v$$
同样的我们可以写出 $g$ 的转移:
$$g_i = frac{1+(1+g_x+g_i)+(sum_{v in son_x且v neq i}1+f_v+g_i)}
{d[x]}$$
化简可得:
$$g_i = g_x+d[x]+\sum_{v \in son_x且v \neq i}f_v$$
时间复杂度 $O(n)$。
经典问题
- 每次随机⼀个 $[1,n]$ 的整数,问期望几次能凑⻬所有数
设 $x_i$ 表示在选择第 $i$ 个数时能选到新数的期望步数。
$E[S] = \sum_{i = 1}^n E[x_i]$,我们算 $E[x]$
发现 $P[x] = \frac{n-i+1}{n}$,所以有 $E[x] = \frac{n}{n-i+1}$.
$$E[S] = \sum_{i=1}^n \frac{n}{n-i+1} = n\sum_{i=1}^n \frac{1}[n-i+1] \approx O(nlogn)$$
- 随机一个⻓度为 $n$ 个排列 $p$,求 $p[1\cdots i]$ 中 $p[i]$ 是最⼤的数的概率
随机出的前 $i$ 个数,每一个数都可能当做最大值,所以概率是 $\frac{1}{i}$
问满足上⾯那个题的 $i$ 的个数的平⽅的期望?
有点意思。。。
设 $x_i$ 表示第 $i$ 个位置是不是满足限制,那么答案 $S = (\sum_{i=1}^n x_i)^2$。
$E[S] = E[(\sum_{i=1}^n x_i)^2]$
我们发现 $x$ 和 $x^2$ 根本不独立,所以不能直接拆。
我们从初中课本中可以得到 $\sum_{i=1}^n x_i = \sum_{i \neq j} x_ix_j + \sum_{i=1}^n x_i^2$。
式子可以进一步拆成 $E[S] = \sum_{i \neq j}E[x_ix_j]+\sum_{i=1}^n E[x_i^2]$。
由于 $x_i$ 的取值范围为 $\{0,1\}$,所以 $x_i^2 = x_i$。
并且我们注意到 $x_i$ 和 $x_j$ 是独立的!(因为我们如果设 $i<j$,$j$ 保证自己最大后就不会影响它前面的取值)。所以式子简化为:
$E[S] = \sum_{i \neq j}E[x_i]E[x_j] +\sum_{i=1}^n E[x_i]$
注意到 $E[xy] = E[x]E[y] = \frac{1}{xy}$。所以有
$E[S] = \sum_{i \neq j} \frac{1}{ij} + \sum_{i=1}^n \frac{1}{i}$
- 随机一个长度为 $n$ 的排列 $p$,求 $i$ 在 $j$ 的后面的概率
$E= \frac{1}{2}$
原因大概是 $i$ 和 $j$ 的相对位置只有 $i,j$ 和 $j,i$ 两种关系,并且这两种出现概率均等。
- 随机⼀个⻓度为 $n$ 的排列 $p$,求它包含 $w[1 \cdots m]$ 作为⼦序列/连续子序列的概率
子序列:$$\frac{(^n_m)*(n-m)!}{n!} = \frac{\frac{n!}{m!(n-m)!}(n-m)!}{n!} = \frac{1}{m!}$$
子串:将要求连续的 $m$ 个元素缩成一个元素:$$\frac{(n-m+1)!}{n!}$$
- 有 $n$ 堆⽯头,第 $i$ 堆个数为 $a[i]$,每次随机选一个⽯头然后把那一整堆都扔了,求第 $1$ 堆石头期望第几次被扔
我们设 $A_i$ 表示第 $i$ 个石头被扔的时间,那么有 $A_1 = (\sum_{i=1}^n [A_i < A_1]) + 1$
求期望:
$$E[A_1] = \sum_{i=1}^n E[[A_i<A_1]] + 1$$
$[exp]$ 取值是 $\{0,1\}$。所以我们就可以算一下概率。只需要考虑这两个数谁先被选,其他的先后关系无关(因为概率比值是始终不变的)
$$E[[A_i<A_1]] = P[[A_i<A_1]] = \frac{A_i}{A_1+A_i}$$
所以最终的期望是:
$$E[A_1] = \sum_{i=1}^n \frac{A_i}{A_1+A_i}$$
- 随机⼀个长度为 $n$ 的01串,每个位置是 $1$ 的概率是 $p$ ,定义 $X$ 是每段连续的 $1$ 的长度的平方之和,求 $E[X]$
CF235B
设 $f_i$ 表示填完前 $i$ 位的答案,$g_i$ 表示到第 $i$ 位末尾的期望长度。
$g_i = (g_{i-1}+1)p + 0*(1-p)$
$f_i = p(f_{i-1}-g_{i-1}^2+g_i^2)+(1-p)f_{i-1}$
通过进一步化简可以得到 $f_{i} = p(f_{i-1}+2g_{i-1}+1)+(1-p)f_{i-1}$
- 给一个序列,每次随机删除⼀个元素,问 $i$ 和 $j$ 在过程中相邻的概率
转成删除序列,发现只需要考虑区间 $[i,j]$ 中 $i,j$ 是否是最后两个被删除的。
组合数学一下发现答案是 $\frac{2*(j-i-1)!}{(j-i+1)!} = \frac{2}{(j-i)(j-i+1)}$
- 给定⼀棵树,将他的边随机⼀个顺序后依次插入,求 $u,v$ 期望什么时候连通
设 $k = dis(u,v)$.我们枚举在 $i$ 时刻恰好联通,期望就是:
$$\sum_{i=k}^{n-1} i\frac{k!\left(^{i-1}_{k-1}\right)(n-1-k)!}{(n-1)!}$$
- 给 $1 \cdots n$ 这 $n$ 个数,每次随机选择⼀个还在的数并且删掉他的所有约数,求期望几次删完
我们考虑删除一个数时,考虑把被影响的数打上标记。如果删除了有标记的数就不对答案造成贡献了。
考虑设随机变量 $x_i$ 表示如果没被打上标记就是 $1$ 其他情况是 $0$。
那么答案就是 $S = \sum_{i=1}^n x_i$
套上期望 $E[S] = \sum_{i=1}^n E[x_i]$
现在我们考虑如何计算 $E[x]$
我们发现 $x$ 没被打标记当且仅当 $x$ 的所有倍数都没有被删除过, $i$ 的倍数个数是 $\lfloor \frac{n}{i} \rfloor$。只考虑这些数被删除的先后顺序,发现概率 $P[x_i] = \frac{1}{\lfloor \frac{n}{i} \rfloor}$,所以 $E[x_i] = P[x_i] = \frac{1}{\lfloor \frac{n}{i} \rfloor}$
所以 $$E[S] = \sum_{i=1}^n \frac{1}{\lfloor \frac{n}{i} \rfloor}$$
练习题
- 给定 $n$ 个硬币,第 $i$ 个硬币的价值为 $w[i]$,每次随机取走一个硬币,获得的收益是左右两个硬币的价值的乘积,求期望总价值
设 $x_{i,j}$ 表示对 $i,j$ 是否对答案造成贡献,答案可以表示为:
$$S = \sum_{1 \leq i,j \leq n} x_{i,j}w_iw_j$$
套上期望,现在只需要求 $E[x_{i,j}]$
发现取值为 $\{0,1\}$,所以值等于概率,也就是这两个在删除过程中相邻的概率,是 $\frac{2}{(j-i)(j-i+1)}$
所以
$$S = \sum_{q \leq i,j \leq n} \frac{2}{(j-i)(j-i+1)} w_iw_j$$
- 有 $n$ 个数 $a[1 \cdots n]$,每次等概率选出两个数,然后合并成一个新的数放回来,得到的收益是新的数的值,求总收益的期望
设 $x_i$ 表示 $i$ 对答案贡献了多少次(也就是被合并了多少次)
$S = \sum_{i=1}^n x_ia_i$
现在也就是要求 $E[x_i]$
考虑在第 $j$ 次 $x_i$ 被合并的概率是 $\frac{2}{n-j+1}$。(因为在第 $j$ 次有 $n-j+1$ 个团,每一次选中的概率都是 $\frac{1}{n-j+1}$)
所以我们就可以得到 $E[x_i] = \sum_{j=1}^{n-1} \frac{1}{n-j+1}$
$E[S] = \sum_{i=1}^n a_i\sum_{j=1}^{n-1} \frac{1}{n-j+1}$
- 给定一个数列 $W[1 \cdots N]$,随机⼀个排列 $H$,如果 $H[i]$ ⽐ $H[i-1]$ 和 $H[i+1]$ 都大,就获得 $W[i]$ 的收益,求期望收益
设随机变量 $x_i$ 表示第 $i$ 位是否对答案产生贡献。只需要算 $E[x_i]$
发现这个大小关系是独立的。所以
begin{align*}
E[x] = left{ begin{array} { l l } { frac{1}{3} , } & { 1 < x,x < n ,} \ { frac{1}{2} } & {text{otherwise}.} end{array} right.
end{align*}
- 给出⼀棵树,一开始每个点都是⽩的,每次选一个白点将他子树里所有点染黑,求期望⼏次染黑整个树
和上面的差不多,删除的时候转而打标记即可。
所以 $E[x] = \frac{1}{dep_i}$
$$E[S] = \sum_{i=1}^n \frac{1}{dep_i}$$
其他小题
- 有 $n$ 个球,⼀开始颜色是 $c[1 \cdots n]$,每次随机一对数 $(i,j)$ 然 后 c[j]=c[i],求让 $c$ 全部相同的期望步数 $n \leq 10^6$
考虑将所有贡献分摊到球上,一次操作 $c_j \to c_i$ 可以让 $i$ 和 $j$ 都加一。答案就 $/2$。
如果我们考虑让颜色都变成 $x$,我们设 $f_A$ 表示已经有了 $A$ 个颜色 $x$ 的期望。
我们首先可以通过简单计算得到下一次染色导致不变的概率 $p_0$,个数加 $1$ 的概率 $p_1$,个数减 $1$ 的概率 $p_{-1}$
那么有转移方程
$$f_A = p_0(f_A+1)+p_1(f_{A-1}+1)+p_{-1}(f_{A+1}+1)$$
- 给定⼀个⻓度为 $n$ 的 01 串,每次随机⼀个区间将里面所有元素翻转,求 $m$ 次操作后 $1$ 的期望个数
$n \leq 10^5,m \leq 10^9$
考虑答案 $S = \sum_{i=1}^n x_i$,那么现在需要求 $E[x_i]$
考虑一个dp $f_{i,0/1}$ 表示求随机翻转 $i$ 次后,是 $0/1$ 的概率。
我们可以通过简单计算算出这次区间包含这个点的概率 $p$,转移就是
$$f_{i,j} = p* f_{i-1,!j} + (1-p)* f_{i-1,j}$$
可以用矩阵乘法优化。
- 给 $n$ 个点,随机选一个点集,求二维凸包的期望点数,保证没有三点共线
$1 \leq n \leq 200$
考虑在最后的凸包中我们设随机变量 $x_{i,j}$ 表示 $i$ 和 $j$ 是否有连边。
那么答案 $S = \sum_{i,j} x_{i,j}$
所以我们要求 $E[x_{i,j}]$,也就要求出 $P[x_{i,j}]$
考虑一条边成为凸包的一条边,当且仅当其他的点都在这个边的一侧。考虑处理出直线左右半平面上点的数量,记为 $s1,s2$,那么 $P[x_{i,j}] = \frac{2^{s1}+2^{s2}}{2^n}$
- 单选错位(P1297)
设 $x_i$ 表示 $i$ 题目是否做对,那么只需要求 $E[x_i] = P[x_i]*1$了。
如果错位后的答案要正确,当且仅当错位前的答案等于错位后的答案,所以不考虑循环边界的概率 $P[x_i] = \frac{\min(w_i,w_{i-1})}{w_{i-1}w_i}$
- ZROI450
设状态 $f_{i,j}$ 表示考虑到第 $i$ 个人,有 $j$ 个人开枪(也就是活着离开了)的概率。
转移时我们先搞出上一个人不死的概率 $q = (1-p)^i$,转移枚举这一个人死不死:
$$f_{i,j} = (1-q)f_{i-1,j}+qf_{i-1,j-1}$$
