后缀自动机学习笔记

Author： RainAir
发布时间：January 28, 2020
1521views
No comments
5371 words
Categories：学习笔记

作为菜鸡 OIer，本文尽量用通俗的语言去讲解后缀自动机。
当然学习后缀自动机前是有一点点前置知识的，我一块给说了。

有限状态自动机（DFA

定义

确定优先状态自动机 $\mathcal{A}$ 是由：

一个非空有限的状态集合 $Q$
一个输入字母表$\Sigma$ （非空有限的字符集合）
一个转移函数 $\delta :Q\times \Sigma \rightarrow Q$（例如：$\delta \left(q,\sigma \right)=p,\left(p,q\in Q,\sigma \in \Sigma \right)$）
一个开始状态$s\in Q$
一个接受状态的集合$F\subseteq Q$
所组成的5-元组，可写成形式 $\mathcal{A} = (Q,\Sigma,\delta,s,F)$

工作方式

确定有限状态自动机从起始状态开始，一个字符接一个字符地读入一个字符串 $w\in \Sigma ^{ * }$（这里的$*$指示Kleene星号算子。），并根据给定的转移函数一步一步地转移至下一个状态。在读完该字符串后，如果该自动机停在一个属于F的接受状态，那么它就接受该字符串，反之则拒绝该字符串。
(以上摘自Wiki)

后缀自动机（SAM）

定义

字符串 $s$ 的后缀自动机是一个接受字符串所有后缀的最小 DFA。（实际上显然可以看出它接受所有 $s$ 的子串）
相信有了上面的铺垫大家定义都懂了，接下来我们学习如何构造 SAM

构造

如果不需要保证是最小 DFA，我们直接把所有后缀插入 trie 就可以了。但是我们实际上是有一个线性构造出 SAM 的方法的。为了介绍这个方法，我们需要引入一些定义。
定义 1：对于一个子串 $p$，我们将其在原串中所有结束位置构成的集合称之为 $endpos(p)$。例如 $s = abbab$，$endpos(ab) = \{2,5\}$

引理 1.1: 如果两个子串的 $endpos$ 相同，那么一个一定是另一个的后缀

证明是显然的。设这两个字符串为 $p,q$，令$|p| \leq |q|$，那么命题不成立时，两个子串在后 $|p|]$ 位上一定有一位不同，但是因为 endpos 相同，那么后 $len_p$ 一定都相同，自己画个图就明白了。

引理 1.2: 对于任意两个子串 $p,q$，令 $|p| \leq |q|$，要么 $endpos(q) \subseteq endpos(p)$，要么 $endpos(p) \cap endpos(q) = \emptyset$

如果 $p$ 是 $q$ 的后缀，那么每次 $q$ 出现一定伴随着 $p$ 出现，所以 $endpos(q) \subseteq endpos(p)$，否则交集一定为空（交集不为空表示存在一个位置他们同时出现，即 $p$ 是 $q$ 后缀）

引理 1.3: 对于 $endpos$ 相同的子串我们将其归为一个 $endpos$ 等价类，将字符串按照长度从大到小排序，则一个字符串总是比它上一个字符串的长度少 $1$，且是上一个的后缀

连续运用引理 1.1 即可。

引理 1.4: $endpos$ 等价类的大小为 $O(n)$

对于一个类，根据引理1.3，我们找到最长的一个子串 $p$，在前面添加一个字符（满足新字符串是原串子串），得到的字符串$q$一定不属于此类，并且由于 $p$ 是新串的后缀，一定有 $endpos(q) \subseteq endpos(p)$，并且添加两个不同的字符，它们的 $endpos$ 也不会有交。所以我们认为向前加入一个字符就是对 $endpos$ 进行分割。所以我们可以按照分割结构建出一个树，可以称为 parents数（fail 树）。
例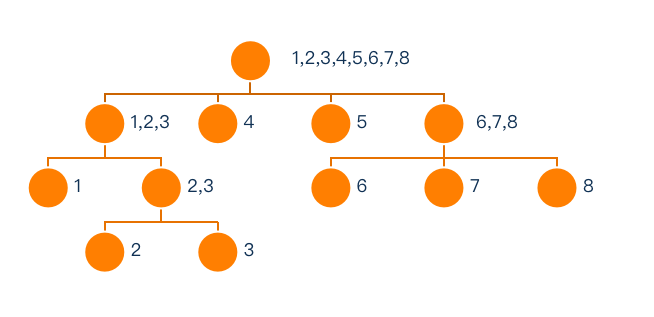： testtest

引理 1.5: 一个类 $a$ 中，令最长子串的长度为 $len(a)$，最短子串长度为 $minlen(a)$，令这个类的父亲为 $fa(a)$，则有 $len(fa(a))+1=minlen(a)$

显然。加上一个新字符后 $endpos$ 缩小，可能会有新的字符串加入。（想象这些字符串原来因为只是 $endpos$ 的子集而未能加入）

现在我们回顾定义：发现我们的 SAM 中的状态只需要由这些等价类来构成就好了。（因为这个可以接受且仅接受所有的子串）我们只需要合理安排一些转移边让这些状态之间可以转化，就可以构造出 SAM。
引理1.4 已经证明了 SAM 的状态数为 $O(n)$，接下来我们证边数为 $O(n)$

引理1.6 SAM 的转移边数为 $O(n)$

假设我们现在有了一个 SAM 的所有边，我们求出任意一棵生成树。
我们对于每个终止节点，考虑按照后缀自动机的边的反向跑，尝试跑出它能接受的所有串。如果这次能顺利跑回源点，那么我们尝试跑下一个子串;如果这次在中间卡掉了，那么我们链上没有的那条边继续跑回源点。这样即使增加后跑出的串不是你想要的那个，但一定是能接受的串中还没跑过的。发现每个结束状态跑的时候加入的边不会超过 $endpos$ 的大小。所以边增加后缀的的个数 $n$，即数量级为 $O(n)$

如何构造

考虑每个节点存储的信息应该有：$ch[],len,fail$。$ch[]$ 存储转移边，$len$ 存储这个等价类最长长度的大小，$fail$ 存储这个等价类在 parent 树（依个人习惯以后将其称之为 fail 树）上的祖先。
我们的构造是一个在线算法，比较好用。
还是感觉这个东西对着程序讲比较简单。

int ch[MAXN][26],fail[MAXN],len[MAXN];

int las = 1,tot = 1;

inline void copy(int x,int y){
    FOR(i,0,25) ch[x][i] = ch[y][i];
    fail[x] = fail[y];len[x] = len[y];
}

inline void insert(int c){
    int p = las;int np = las = ++tot;
    len[np] = len[p]+1;
    while(p&amp;&amp;!ch[p][c]) ch[p][c] = np,p = fail[p];
    if(!p) fail[np] = 1;
    else{
        int q = ch[p][c];
        if(len[p]+1 == len[q]) fail[np] = q;
        else{
            int nq = ++tot;copy(nq,q);// split
            len[nq] = len[p]+1;
            fail[q] = fail[np] = nq;
            while(p&amp;&amp;ch[p][c]==q) ch[p][c] = nq,p = fail[p];
        }
    }
}
char str[MAXN];
int main(){
    scanf("%s",str+1);int n = strlen(str+1)；
    FOR(i,1,n) insert(str[i]);
    return 0;
}

我们来记住下 SAM 中两类边的用途：

SAM 上的边，走一步相当于在字符串后面加上字符后的最大等价类，加入字符之后需要尽量向前扩展（向前扩展的另一个解释详见引理1.5）
fail 树上的边，走一步相当于找最大的$endpos$不同的后缀。
我们开始分步讲解 insert 函数。

int p = las;int np = las = ++tot;
len[np] = len[p]+1;

$p$ 存插入前 SAM 中原串组成的等价类的点，$np$ 存插入后的。
$len$ 的转移显然。

while(p&&!chp) chp = np,p = fail[p];

这个时候 $p$ 所有后缀并且无法通过 $c$ 字符转移的可以通过现在新加入的 $c$ 转移了，我们更新一下边。我们会找到第一个节点满足它已经有能转移加 $c$ 的边为止。

if(!p) fail[np] = 1;

一直都没有找到，说明 $c$ 没有出现过，直接更新 fail 为空串即可。

else{
    int q = chp;
    if(len[p]+1 == len[q]) fail[np] = q;

找到了这样的点，于是我们找到按照 $c$ 直接转移下去的点。
如果 $len_p+1=len_q$，说明加入 $c$ 后向前扩展失败，$q$ 的所有子串都会是 $np$ 的子串的后缀，更新 fail 即可。

else{
    int nq = ++tot;copy(nq,q);// split
    len[nq] = len[p]+1;
    fail[q] = fail[np] = nq;
    while(p&&chp==q) chp = nq,p = fail[p];
}

如果扩展出来了新的就麻烦了。我们考虑将这个点拆成两个点：一个是我们想要的没有扩展出新的字符串的点，另一个是只包含扩展出新的字符串的点，这样不影响 SAM 的性质。
我们设我们拆出的子集想要的点为 $nq$，首先 $nq$ 的所有转移边和 $q$ 都一样（原来就是 q 的一部分），然后我们更新 $nq$ 的 len 为我们想要的len。这样 $np$ 的 fail 就可以更新了，不过注意只包含扩展出新的字符串的点的 fail 需要更新成 $nq$（更长的的不同状态的后缀）。
最后那个循环：考虑之前所有转移到未拆的点上的边，现在只能转移到那个我们想要的点上，不能转移到只包含扩展出新的字符串的点（否则会出现新的字符串）。所以我们需要更新一下这些字符串的 fail。
构造过程大概就是这样，如果想手动模拟可以看一下咕咕日报链接后面专门有一部分带你手动模拟建立 SAM，博主由于太咕加上本来很好懂就不写了。

简单运用

判断一个字符串是否出现

使用 DFA 的定义来判断是否接受该字符串。

不同子串个数

后缀自动机不会存相同的字符串，所以答案是 $$\sum_{i} (len(i)-len(fa(i)))$$

第k大子串

首先 SAM 是个 DAG，可以 dp 出 $f_i$ 表示 i 到结束节点包含的子串的个数：
$f_i = \sum f_{to}+len_{to}-len_{i}$
然后类似于权值线段树查询 $k$ 大的写法即可。

最小表示法

设字符串为$S$，我们对 $S+S$ 建立 SAM，只需要找到长度为 $|S|$ 字典序最小的串。可以贪心走最小的边实现。

某个子串的出现次数

首先从 SAM 上走定位到相应节点出现次数就是子树内代表一个后缀的节点的个数
如果我们想快速支持在头部删除一个节点的话只需要记录当前的长度当长度和 fail 的最长一样的时候就跳到 fail 注意有一些细节
比如 CF235C:就需要先插入后删除并且只有在长度>l 的时候才删除（否则匹配的一定是个真后缀就不用从当前点所代表的字符串删除了）
如果我们想快速支持在尾部删除一个节点的话保存下来所有的路径就可以了

子串第一次出现的位置

同理对子树内代表一个后缀的编号取 min
待更。。。

Last modification：April 14th, 2020 at 04:06 pm

如果觉得我的文章对你有用，请随意赞赏

后缀自动机学习笔记

RainAir • 2020 年 01 月 28 日

作为菜鸡 OIer，本文尽量用通俗的语言去讲解后缀自动机。
当然学习后缀自动机前是有一点点前置知识的，我一块给说了。

有限状态自动机（DFA

定义

确定优先状态自动机 $\mathcal{A}$ 是由：

一个非空有限的状态集合 $Q$
一个输入字母表$\Sigma$ （非空有限的字符集合）
一个转移函数 $\delta :Q\times \Sigma \rightarrow Q$（例如：$\delta \left(q,\sigma \right)=p,\left(p,q\in Q,\sigma \in \Sigma \right)$）
一个开始状态$s\in Q$
一个接受状态的集合$F\subseteq Q$
所组成的5-元组，可写成形式 $\mathcal{A} = (Q,\Sigma,\delta,s,F)$

工作方式

后缀自动机（SAM）

定义

构造

引理 1.1: 如果两个子串的 $endpos$ 相同，那么一个一定是另一个的后缀

引理 1.2: 对于任意两个子串 $p,q$，令 $|p| \leq |q|$，要么 $endpos(q) \subseteq endpos(p)$，要么 $endpos(p) \cap endpos(q) = \emptyset$

连续运用引理 1.1 即可。

引理 1.4: $endpos$ 等价类的大小为 $O(n)$

引理 1.5: 一个类 $a$ 中，令最长子串的长度为 $len(a)$，最短子串长度为 $minlen(a)$，令这个类的父亲为 $fa(a)$，则有 $len(fa(a))+1=minlen(a)$

显然。加上一个新字符后 $endpos$ 缩小，可能会有新的字符串加入。（想象这些字符串原来因为只是 $endpos$ 的子集而未能加入）

引理1.6 SAM 的转移边数为 $O(n)$

如何构造

int ch[MAXN][26],fail[MAXN],len[MAXN];

int las = 1,tot = 1;

inline void copy(int x,int y){
    FOR(i,0,25) ch[x][i] = ch[y][i];
    fail[x] = fail[y];len[x] = len[y];
}

inline void insert(int c){
    int p = las;int np = las = ++tot;
    len[np] = len[p]+1;
    while(p&amp;&amp;!ch[p][c]) ch[p][c] = np,p = fail[p];
    if(!p) fail[np] = 1;
    else{
        int q = ch[p][c];
        if(len[p]+1 == len[q]) fail[np] = q;
        else{
            int nq = ++tot;copy(nq,q);// split
            len[nq] = len[p]+1;
            fail[q] = fail[np] = nq;
            while(p&amp;&amp;ch[p][c]==q) ch[p][c] = nq,p = fail[p];
        }
    }
}
char str[MAXN];
int main(){
    scanf("%s",str+1);int n = strlen(str+1)；
    FOR(i,1,n) insert(str[i]);
    return 0;
}

我们来记住下 SAM 中两类边的用途：

SAM 上的边，走一步相当于在字符串后面加上字符后的最大等价类，加入字符之后需要尽量向前扩展（向前扩展的另一个解释详见引理1.5）
fail 树上的边，走一步相当于找最大的$endpos$不同的后缀。
我们开始分步讲解 insert 函数。

int p = las;int np = las = ++tot;
len[np] = len[p]+1;

$p$ 存插入前 SAM 中原串组成的等价类的点，$np$ 存插入后的。
$len$ 的转移显然。

while(p&&!chp) chp = np,p = fail[p];

if(!p) fail[np] = 1;

一直都没有找到，说明 $c$ 没有出现过，直接更新 fail 为空串即可。

else{
    int q = chp;
    if(len[p]+1 == len[q]) fail[np] = q;

else{
    int nq = ++tot;copy(nq,q);// split
    len[nq] = len[p]+1;
    fail[q] = fail[np] = nq;
    while(p&&chp==q) chp = nq,p = fail[p];
}

简单运用

判断一个字符串是否出现

使用 DFA 的定义来判断是否接受该字符串。

不同子串个数

后缀自动机不会存相同的字符串，所以答案是 $$\sum_{i} (len(i)-len(fa(i)))$$

第k大子串

首先 SAM 是个 DAG，可以 dp 出 $f_i$ 表示 i 到结束节点包含的子串的个数：
$f_i = \sum f_{to}+len_{to}-len_{i}$
然后类似于权值线段树查询 $k$ 大的写法即可。

最小表示法

设字符串为$S$，我们对 $S+S$ 建立 SAM，只需要找到长度为 $|S|$ 字典序最小的串。可以贪心走最小的边实现。

某个子串的出现次数

子串第一次出现的位置

同理对子树内代表一个后缀的编号取 min
待更。。。

有限状态自动机（DFA

定义

工作方式

后缀自动机（SAM）

定义

构造

如何构造

简单运用

判断一个字符串是否出现

不同子串个数

第k大子串

最小表示法

某个子串的出现次数

子串第一次出现的位置