众所周知 LCT 可以用来维护动态树的点权信息,但是总有一些题目让你维护动态树上的子树信息或者是链信息,就在这里拿一道经典的题目讲一讲。
<h2>「UOJ207」共价大爷游长沙</h2>
题目链接
题目要求维护动态树和一个路径集合,询问某一条边是否被路径集合中所有的路径经过。
首先我们考虑一下树是静态的怎么做:显然我们可以yy出一个随机化算法,我们可以对于每一条路径 $(u,v)$ ,将该路径的两个端点都异或上一个随机权值 $s$。询问的时候只需要求一下切掉这条边后两边子树的权值是不是等于所有路径的异或和就可以了。
但是我们并不会 LCT 维护原树子树权值啊...这怎么办?
我们首先观察一下一个节点被 access 后的规律:(图源链接)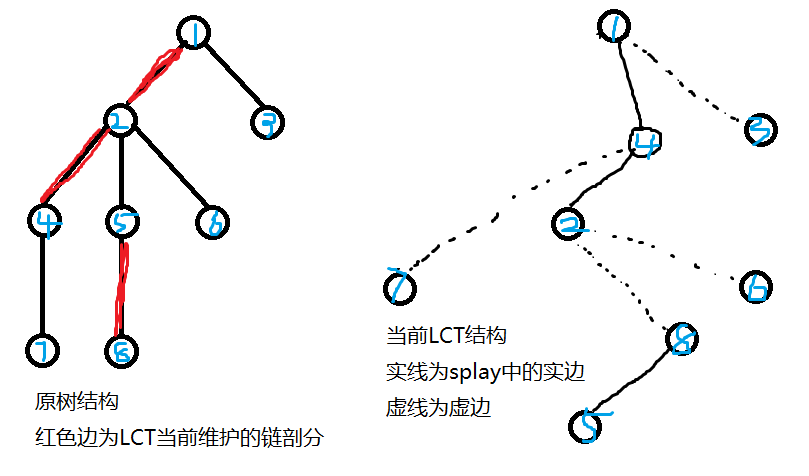
我们定义一个节点在 splay 中的儿子有实儿子和虚儿子,实边连向的儿子就是实儿子,虚边亦然。那么也可以定义出实子树和虚子树,实儿子的子树就是实子树。
现在我们来考虑一下 access 操作吧:对于一个点 $x$ ,它被 access 之后,它的虚子树会包含且仅包含它在原树中子树内除了这个点之外的点。(为什么呢?因为 access 操作实质上是每次将自己的右儿子(子树)断开(变为虚边),所以 access 操作结束后所有的儿子与这个节点连的都是虚边)那么我们只需要附带着维护出 splay 中每一个节点的虚子树信息,就可以维护出原树子树信息了。
那我们来考虑一下如何动态维护虚子树的信息,我们会发现只有在 link 和 access 操作的时候会改变虚子树信息。
我们回顾一下 access 操作的代码:
inline void access(int x){
for(int y=0;x;x = f[y = x]){
splay(x);rc = y;pushup(x);
}
}发现我们在 access 操作中有换儿子的地方,那么考虑换右儿子的时候,原来的右儿子加入到了虚子树,新的右儿子是实子树的一部分了,因此每次应加上原来的右儿子的信息,减去新的右儿子的信息。新的代码如下(以维护树大小 size 为例):
inline void access(int x){
for(int y = 0;x;x = f[y = x]){
splay(x);son[x] += size[rc] - size[y];
rc = y;pushup(x);
}
}我们来考虑一下 link 操作的影响:我们的 link 操作(不特判)是这样写的:
inline void link(int x,int y){
makeroot(x);f[x] = y;
}发现这是 $x$ 向 $y$ 连了一条轻边,即 $x$ 成了 $y$ 的虚子树!所以 $x$ 的信息应该合并到 $y$ 的虚子树信息上。但是 $y$ 的祖先的信息也要更改,这就不能维护了...所以我们也要钦定 $y$ 为根一次,这样就只需要更改 $y$ 节点的信息就可以了。
还是以维护 size 为例:
inline void link(int x,int y){
makeroot(x);makeroot(y);f[x] = y;
son[y] += size[x];pushup(y);
}我们还需要维护一个 x 的 LCT 子树的信息和,x 的 LCT 子树的信息和就等于 x 的实儿子的 LCT 子树信息和加上 x 的虚子树的信息和加上 x 自己,在 splay 的 pushup 函数中就可以直接维护
inline void pushup(int x){
size[x] = size[lc] + size[rc] + son[x] + 1;
}现在这个题目的做法就十分显然啦。我们每次查询的时候把这条边两边的点拿出来,判断一下权值就可以了。
完整代码:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define fi first
#define lc (ch[x][0])
#define se second
#define U unsigned
#define rc (ch[x][1])
#define Re register
#define LL long long
#define MP std::make_pair
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 100000+5;
int ch[MAXN][2],f[MAXN],val[MAXN],sum[MAXN],tag[MAXN],son[MAXN];
inline bool nroot(int x){
return ch[f[x]][0] == x || ch[f[x]][1] == x;
}
inline void reverse(int x){
std::swap(lc,rc);tag[x] ^= 1;
}
inline void pushdown(int x){
if(tag[x]){
if(lc) reverse(lc);
if(rc) reverse(rc);
tag[x] = 0;
}
}
inline void pushup(int x){
sum[x] = sum[lc]^sum[rc]^val[x]^son[x];
}
inline void rotate(int x){
int y = f[x],z = f[y],k = ch[y][1]==x,w = ch[x][!k];
if(nroot(y)) ch[z][ch[z][1]==y] = x;
ch[x][!k] = y;ch[y][k] = w;
if(w) f[w] = y;
f[y] = x;f[x] = z;
pushup(y);
}
int st[MAXN];
inline void splay(int x){
int y = x,z;st[z = 1] = y;
while(nroot(y)) st[++z] = y = f[y];
while(z) pushdown(st[z--]);
while(nroot(x)){
y = f[x],z = f[y];
if(nroot(y)) rotate((ch[y][0] == x)^(ch[z][0]==y) ? x : y);
rotate(x);
}
pushup(x);
}
inline void access(int x){
for(int y = 0;x;x = f[y = x]){
splay(x);son[x] ^= sum[rc]^sum[y];
rc = y;pushup(x);
}
}
inline void makeroot(int x){
access(x);splay(x);reverse(x);
}
inline void link(int x,int y){
makeroot(x);makeroot(y);f[x] = y;
son[y] ^= sum[x];pushup(y);
}
inline void split(int x,int y){
makeroot(x);access(y);splay(y);
}
inline void cut(int x,int y){
split(x,y);f[x] = ch[y][0] = 0;
}
int N,M;
struct Edge{
int u,v,w;
}e[MAXN<<2];
int cnt,S;
int main(){
srand(20050117);
scanf("%*d%d%d",&N,&M);
FOR(i,1,N-1){
int x,y;scanf("%d%d",&x,&y);
link(x,y);
}
while(M--){
int x,y,u,v,opt;scanf("%d%d",&opt,&x);
if(opt == 1){
scanf("%d%d%d",&y,&u,&v);
cut(x,y);link(u,v);
}
if(opt == 2){
scanf("%d",&y);
e[++cnt] = (Edge){x,y,rand()};
makeroot(x);val[x] ^= e[cnt].w;pushup(x);
makeroot(y);val[y] ^= e[cnt].w;pushup(y);
S ^= e[cnt].w;
}
if(opt == 3){
makeroot(e[x].u);val[e[x].u] ^= e[x].w;pushup(e[x].u);
makeroot(e[x].v);val[e[x].v] ^= e[x].w;pushup(e[x].v);
S ^= e[x].w;
}
if(opt == 4){
scanf("%d",&y);split(x,y);
puts(sum[x]^S ? "NO" : "YES");
}
}
return 0;
}<h2>「BZOJ4530」 大融合</h2>
这种题就不单独开一篇文章放了.....
题目链接
题目要求你查询动态树上有多少条路径经过了某一条边,显然答案是这条边两端节点为根的两棵子树的乘积。那就是用 LCT 维护一下子树大小了,上面讲过的例题。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <vector>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#define fi first
#define lc (ch[x][0])
#define se second
#define U unsigned
#define rc (ch[x][1])
#define Re register
#define LL long long
#define MP std::make_pair
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(Re int i = a;i <= b;++i)
#define ROF(i,a,b) for(Re int i = a;i >= b;--i)
#define SFOR(i,a,b,c) for(Re int i = a;i <= b;i+=c)
#define SROF(i,a,b,c) for(Re int i = a;i >= b;i-=c)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
const int MAXN = 100000+5;
int ch[MAXN][2],f[MAXN],son[MAXN],size[MAXN],rev[MAXN];
inline bool nroot(int x){
return ch[f[x]][0] == x || ch[f[x]][1] == x;
}
inline void pushup(int x){
size[x] = size[lc] + size[rc] + son[x] + 1;
}
inline void reverse(int x){
std::swap(lc,rc);rev[x] ^= 1;
}
inline void pushdown(int x){
if(rev[x]){
if(lc) reverse(lc);
if(rc) reverse(rc);
rev[x] = 0;
}
}
inline void rotate(int x){
int y = f[x],z = f[y],k = ch[y][1] == x,w = ch[x][!k];
if(nroot(y)) ch[z][ch[z][1] == y] = x;
ch[x][!k] = y;ch[y][k] = w;
if(w) f[w] = y;
f[y] = x;f[x] = z;
pushup(y);
}
int st[MAXN];
inline void splay(int x){
int y = x,z;st[z = 1] = y;
while(nroot(y)) st[++z] = y = f[y];
while(z) pushdown(st[z--]);
while(nroot(x)){
y = f[x],z = f[y];
if(nroot(y)) rotate((ch[y][0] == x) ^ (ch[z][0] == y) ? x : y);
rotate(x);
}
pushup(x);
}
inline void access(int x){
for(int y = 0;x;x = f[y = x]){
splay(x);son[x] += size[rc] - size[y];
rc = y;pushup(x);
}
}
inline void makeroot(int x){
access(x);splay(x);reverse(x);
}
inline void link(int x,int y){
makeroot(x);makeroot(y);f[x] = y;
son[y] += size[x];pushup(y);
}
int main(){
int N,M;scanf("%d%d",&N,&M);
FOR(i,1,M){
char str[20];int x,y;
scanf("%s%d%d",str+1,&x,&y);
if(str[1] == 'A'){
link(x,y);
}
if(str[1] == 'Q'){
makeroot(x);makeroot(y);
printf("%lld\n",1ll*size[x]*(size[y]-size[x]));
}
}
return 0;
}
4 comments
Orz
Orz!
wyh TQL
Orz